Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, đạo hàm để giải quyết các vấn đề thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin làm bài.
Tìm đạo hàm của mỗi hàm số sau :
\(\displaystyle y = {{\sin x} \over x} + {x \over {{\mathop{\rm sinx}\nolimits} }}\)
Phương pháp giải:
Sử dụng công thức đạo hàm hàm hợp và các công thức tính đạo hàm các hàm số sơ cấp.
Giải chi tiết:
\(y' = \dfrac{{\left( {\sin x} \right)'.x - \sin x.\left( {x'} \right)}}{{{x^2}}}\) \( + \dfrac{{x'\sin x - x.\left( {\sin x} \right)'}}{{{{\sin }^2}x}}\)
\(\eqalign{ & = {{x\cos x - \sin x} \over {{x^2}}} + {{\sin x - x\cos x} \over {{{\sin }^2}x}} \cr & = \left( {x\cos x - {\mathop{\rm sinx}\nolimits} } \right)\left( {{1 \over {{x^2}}} - {1 \over {{{\sin }^2}x}}} \right) \cr} \)
\(\displaystyle y = {{{{\sin }^2}x} \over {1 + \tan 2x}}\)
Phương pháp giải:
Sử dụng công thức đạo hàm hàm hợp và các công thức tính đạo hàm các hàm số sơ cấp.
Giải chi tiết:
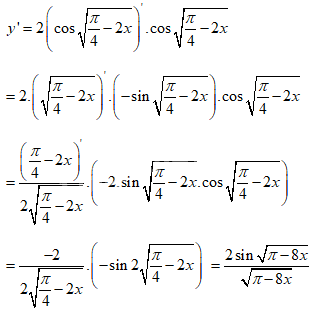
\(y = \tan \left( {\sin x} \right)\)
Phương pháp giải:
Sử dụng công thức đạo hàm hàm hợp và các công thức tính đạo hàm các hàm số sơ cấp.
Giải chi tiết:
\(y' = \left( {\sin x} \right)'.\dfrac{1}{{{{\cos }^2}\left( {\sin x} \right)}}\) \( \displaystyle = {{\cos x} \over {{{\cos }^2}\left( {\sin x} \right)}}\)
\(y = x\cot \left( {{x^2} - 1} \right)\)
Phương pháp giải:
Sử dụng công thức đạo hàm hàm hợp và các công thức tính đạo hàm các hàm số sơ cấp.
Giải chi tiết:
\(y' = x'.\cot \left( {{x^2} - 1} \right) + x.\left[ {\cot \left( {{x^2} - 1} \right)} \right]'\) \( = \cot \left( {{x^2} - 1} \right) + x.\left( {{x^2} - 1} \right)'.\dfrac{{ - 1}}{{{{\sin }^2}\left( {{x^2} - 1} \right)}}\)
\(\eqalign{ & = \cot \left( {{x^2} - 1} \right) + x.{{ - 2x} \over {{{\sin }^2}\left( {{x^2} - 1} \right)}} \cr & = \cot \left( {{x^2} - 1} \right) - {{2{x^2}} \over {{{\sin }^2}\left( {{x^2} - 1} \right)}} \cr} \)
\(\displaystyle y = {\cos ^2}\sqrt {{\pi \over 4} - 2x} \)
Phương pháp giải:
Sử dụng công thức đạo hàm hàm hợp và các công thức tính đạo hàm các hàm số sơ cấp.
Giải chi tiết:
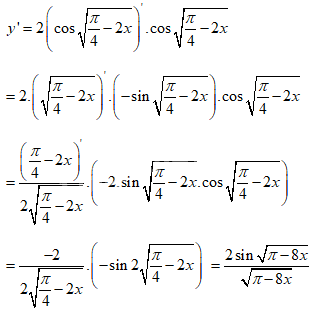
\(y = x\sqrt {\sin 3x} \)
Phương pháp giải:
Sử dụng công thức đạo hàm hàm hợp và các công thức tính đạo hàm các hàm số sơ cấp.
Giải chi tiết:
\(y' = x'\sqrt {\sin 3x} + x.\left( {\sqrt {\sin 3x} } \right)'\) \( = \sqrt {\sin 3x} + x.\dfrac{{\left( {\sin 3x} \right)'}}{{2\sqrt {\sin 3x} }}\) \( \displaystyle = \sqrt {\sin 3x} + x.{{3\cos 3x} \over {2\sqrt {\sin 3x} }} \) \(\displaystyle = {{2\sin 3x + 3x\cos 3x} \over {2\sqrt {\sin 3x} }}\)
Câu 33 trang 212 SGK Đại số và Giải tích 11 Nâng cao thuộc chương trình học kỳ I, lớp 11. Bài toán này thường liên quan đến việc xét tính đơn điệu của hàm số, tìm cực trị, hoặc giải phương trình, bất phương trình chứa đạo hàm. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, các quy tắc tính đạo hàm, và các phương pháp xét tính đơn điệu của hàm số.
Trước khi bắt đầu giải bài toán, điều quan trọng là phải đọc kỹ đề bài, hiểu rõ yêu cầu của bài toán. Xác định rõ hàm số cần xét, khoảng xác định của hàm số, và các yêu cầu cụ thể của bài toán (ví dụ: tìm cực trị, xét tính đơn điệu, giải phương trình, bất phương trình).
Giả sử bài toán yêu cầu tìm cực trị của hàm số f(x) = x3 - 3x2 + 2.
Ngoài bài toán tìm cực trị, Câu 33 trang 212 có thể yêu cầu học sinh xét tính đơn điệu của hàm số, giải phương trình, bất phương trình chứa đạo hàm. Đối với các bài toán này, học sinh cần áp dụng các kiến thức và phương pháp đã học một cách linh hoạt và sáng tạo.
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, học sinh nên làm thêm các bài tập tương tự trong SGK, sách bài tập, và các đề thi thử. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và tự tin làm bài trong các kỳ thi.
Giaitoan.edu.vn cung cấp đầy đủ lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Đại số và Giải tích 11 Nâng cao. Ngoài ra, chúng tôi còn cung cấp các bài giảng video, bài tập trắc nghiệm, và các tài liệu học tập khác để giúp bạn học tập hiệu quả hơn. Hãy truy cập giaitoan.edu.vn ngay hôm nay để khám phá!
| Hàm số y | Đạo hàm y' |
|---|---|
| y = c (hằng số) | y' = 0 |
| y = xn | y' = nxn-1 |
| y = sinx | y' = cosx |
| y = cosx | y' = -sinx |