Giải Câu 20 Trang 23 SGK Hình học 11 Nâng cao

Câu 20 trang 23 SGK Hình học 11 Nâng cao

Giải Bài Tập Hình Học 11 Nâng cao - Câu 20 Trang 23

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Hình học 11 Nâng cao.

Bài viết này sẽ hướng dẫn bạn giải Câu 20 trang 23 SGK Hình học 11 Nâng cao một cách dễ hiểu nhất, giúp bạn nắm vững kiến thức và kỹ năng giải toán.

Chúng tôi cam kết cung cấp nội dung chất lượng cao, được kiểm duyệt bởi đội ngũ giáo viên giàu kinh nghiệm.

Chứng tỏ rẳng hai hình chữ nhật cùng kích thước (cùng chiều dài và chiều rộng) thì bằng nhau

Đề bài

Chứng tỏ rẳng hai hình chữ nhật cùng kích thước (cùng chiều dài và chiều rộng) thì bằng nhau

Lời giải chi tiết

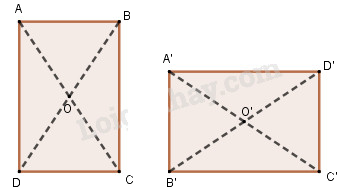
Câu 20 trang 23 SGK Hình học 11 Nâng cao 1

Giả sử hai hình chữ nhật ABCD và A’B’C’D’ có \(AB = CD = A’B’= C’D’, \)\(AD = BC = A’D = B’C’\).

Khi đó ABC và A’B’C’ là hai tam giác vuông bằng nhau, do đó có phép dời hình F biến tam giác ABC thành tam giác A’B’C’

Khi đó phép dời hình F biến trung điểm O của AC thành trung điểm O’ của A’C’

Nhưng vì O và O’ lần lượt cũng là trung điểm của BD và B’D’ nên F cũng biến D thành D’

Vậy F biến ABCD thành A’B’C’D’, nên theo định nghĩa, hai hình chữ nhật đó bằng nhau

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Câu 20 trang 23 SGK Hình học 11 Nâng cao – hành trang không thể thiếu trong chuyên mục Ôn tập Toán lớp 11 trên nền tảng môn toán. Bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Câu 20 Trang 23 SGK Hình Học 11 Nâng Cao: Phân Tích Chi Tiết và Hướng Dẫn Giải

Câu 20 trang 23 SGK Hình học 11 Nâng cao thường liên quan đến các kiến thức về vectơ, đặc biệt là các phép toán vectơ trong không gian. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:

Vectơ: Định nghĩa, các đặc trưng của vectơ (độ dài, hướng).
Phép cộng, trừ vectơ: Quy tắc hình bình hành, quy tắc tam giác.
Phép nhân vectơ với một số thực: Tính chất, ứng dụng.
Tích vô hướng của hai vectơ: Định nghĩa, công thức tính, ứng dụng để tính góc giữa hai vectơ, kiểm tra vuông góc.
Hệ tọa độ trong không gian: Biểu diễn vectơ bằng tọa độ, các phép toán vectơ trong hệ tọa độ.

Phân Tích Đề Bài và Xác Định Chiến Lược Giải

Trước khi bắt tay vào giải, hãy đọc kỹ đề bài và xác định rõ:

Yêu cầu của bài toán: Tính độ dài, tìm góc, chứng minh đẳng thức vectơ, hay xác định vị trí tương đối của các điểm?
Dữ kiện đã cho: Các vectơ đã cho, tọa độ các điểm, các mối quan hệ giữa các vectơ.
Kiến thức cần sử dụng: Các công thức, định lý, tính chất nào liên quan đến yêu cầu của bài toán?

Sau khi phân tích đề bài, hãy xây dựng một chiến lược giải cụ thể, bao gồm các bước thực hiện và các công cụ hỗ trợ.

Hướng Dẫn Giải Chi Tiết Câu 20 Trang 23 (Ví dụ Minh Họa)

Giả sử Câu 20 trang 23 SGK Hình học 11 Nâng cao có nội dung như sau:

Cho hai vectơ \vec{a} = (1; 2; -1) và \vec{b} = (-2; 0; 3). Tính:

\vec{a} + \vec{b}
2\vec{a} - \vec{b}
\vec{a} \cdot \vec{b}

Giải:

\vec{a} + \vec{b} = (1 + (-2); 2 + 0; -1 + 3) = (-1; 2; 2)
2\vec{a} - \vec{b} = (2(1) - (-2); 2(2) - 0; 2(-1) - 3) = (4; 4; -5)
\vec{a} \cdot \vec{b} = (1)(-2) + (2)(0) + (-1)(3) = -2 + 0 - 3 = -5

Các Dạng Bài Tập Liên Quan và Phương Pháp Giải

Ngoài dạng bài tập tính toán vectơ, Câu 20 trang 23 và các bài tập lân cận thường xuất hiện các dạng bài tập sau:

Chứng minh đẳng thức vectơ: Sử dụng các quy tắc phép toán vectơ, các tính chất của tích vô hướng.
Tìm điều kiện để các vectơ cùng phương, vuông góc: Sử dụng tích vô hướng, hệ số tỉ lệ.
Ứng dụng vectơ vào hình học không gian: Tính góc giữa đường thẳng và mặt phẳng, khoảng cách từ điểm đến mặt phẳng.

Để giải quyết các dạng bài tập này, học sinh cần:

Nắm vững lý thuyết: Hiểu rõ các định nghĩa, công thức, định lý liên quan.
Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và kinh nghiệm.
Sử dụng sơ đồ hình học: Vẽ hình minh họa để trực quan hóa bài toán và tìm ra hướng giải.

Lời Khuyên và Tài Liệu Tham Khảo

Để học tốt môn Hình học 11 Nâng cao, bạn nên:

Đọc kỹ sách giáo khoa: Nắm vững kiến thức cơ bản và các ví dụ minh họa.
Làm bài tập đầy đủ: Rèn luyện kỹ năng giải toán và củng cố kiến thức.
Tìm kiếm sự giúp đỡ khi cần thiết: Hỏi giáo viên, bạn bè hoặc tham gia các diễn đàn học tập trực tuyến.

Ngoài sách giáo khoa, bạn có thể tham khảo thêm các tài liệu sau:

Sách bài tập Hình học 11 Nâng cao: Cung cấp nhiều bài tập đa dạng và phong phú.
Các trang web học toán online: giaitoan.edu.vn, VietJack, Hoc24...
Các video bài giảng Hình học 11 Nâng cao: Trên YouTube, Vimeo...

Kết Luận

Câu 20 trang 23 SGK Hình học 11 Nâng cao là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và rèn luyện kỹ năng giải toán. Hy vọng với hướng dẫn chi tiết và các lời khuyên trên, bạn sẽ giải quyết bài toán này một cách dễ dàng và hiệu quả. Chúc bạn học tốt!