Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, đường thẳng và mặt phẳng để giải quyết các vấn đề thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin làm bài.
Cho hình hộp ABCD.A’B’C’D’. Điểm M nằm giữa A và D, điểm N nằm giữa C và C’ sao cho
Đề bài
Cho hình hộp ABCD.A’B’C’D’. Điểm M nằm giữa A và D, điểm N nằm giữa C và C’ sao cho \({{AM} \over {MD}} = {{CN} \over {NC'}}\)
a. Chứng minh rằng đường thẳng MN song song với mp(ACB’)
b. Xác định thiết diện của hình hộp khi cắt bởi mặt phẳng đi qua MN và song song với mp(ACB’)
Lời giải chi tiết
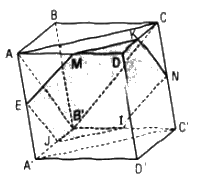
a. \({{AM} \over {MD}} = {{CN} \over {NC'}} \Rightarrow {{AM} \over {CN}} = {{MD} \over {NC'}} = {{AD} \over {CC'}}\)
theo định lí Ta-lét đảo thì MN song song mp(P), ở đó (P) song song với AC và DC’
Mặt khác DC’ // AB’. Vậy MN // (ACB’)
b. Kẻ MK // AC (K ϵ CD); kẻ NI // CB’ (I ϵ C’B’); kẻ IJ // A’C’ (J ϵ A’B’) ;
Kẻ JE // AB’ (E ϵ AA’).
Thiết diện là lục giác MKNIJE.
Câu 5 trang 125 SGK Hình học 11 Nâng cao thuộc chương trình học Hình học không gian, cụ thể là phần liên quan đến vectơ, đường thẳng và mặt phẳng trong không gian. Bài tập này thường yêu cầu học sinh phải vận dụng các kiến thức đã học để chứng minh một đẳng thức vectơ, xác định mối quan hệ giữa các điểm, đường thẳng và mặt phẳng, hoặc tính toán các đại lượng hình học.
Để hiểu rõ hơn về bài tập này, chúng ta cần xem lại nội dung cụ thể của Câu 5 trang 125 SGK Hình học 11 Nâng cao. (Giả sử nội dung bài tập là: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD)).
Để giải bài tập này, chúng ta sẽ sử dụng các phương pháp sau:
Bước 1: Chọn hệ tọa độ
Chọn A làm gốc tọa độ, AB làm trục Ox, AD làm trục Oy, AS làm trục Oz. Khi đó, ta có các tọa độ sau:
Bước 2: Tìm vectơ SC
SC = (a - 0; a - 0; 0 - a) = (a; a; -a)
Bước 3: Tìm vectơ pháp tuyến của mặt phẳng (ABCD)
Mặt phẳng (ABCD) có phương trình z = 0, do đó vectơ pháp tuyến của mặt phẳng (ABCD) là n = (0; 0; 1)
Bước 4: Tính góc giữa SC và mặt phẳng (ABCD)
Gọi α là góc giữa SC và mặt phẳng (ABCD). Ta có:
sin α = |SC.n| / (||SC|| * ||n||)
SC.n = (a; a; -a).(0; 0; 1) = -a
||SC|| = √(a² + a² + (-a)²) = √(3a²)= a√3
||n|| = √(0² + 0² + 1²) = 1
sin α = |-a| / (a√3 * 1) = 1/√3
α = arcsin(1/√3) ≈ 35.26°
Kết luận: Góc giữa đường thẳng SC và mặt phẳng (ABCD) là khoảng 35.26°.
Kiến thức về vectơ, đường thẳng và mặt phẳng trong không gian có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, như:
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự như:
Hy vọng với lời giải chi tiết và những lưu ý trên, bạn đã hiểu rõ hơn về Câu 5 trang 125 SGK Hình học 11 Nâng cao. Chúc bạn học tốt!