Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, đạo hàm để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin làm bài.
Tìm các giới hạn sau :
\(\mathop {\lim }\limits_{x \to + \infty } {{{x^3} - 5} \over {{x^2} + 1}}\)
Lời giải chi tiết:
\(\eqalign{& \mathop {\lim }\limits_{x \to + \infty } {{{x^3} - 5} \over {{x^2} + 1}} = \mathop {\lim }\limits_{x \to + \infty } {x}{{{x^2}\left( {1 - {5 \over {{x^3}}}} \right)} \over {{x^2}\left( {1 + {1 \over {{x^2}}}} \right)}} \cr & = \mathop {\lim }\limits_{x \to + \infty } x.{{1 - {5 \over {{x^3}}}} \over {1 + {1 \over {{x^2}}}}} = + \infty \cr & \text{vì}\,\mathop {\lim }\limits_{x \to + \infty } x = + \infty \,\text{và}\,\mathop {\lim }\limits_{x \to + \infty } {{1 - {5 \over {{x^3}}}} \over {1 + {1 \over {{x^2}}}}} = 1 > 0 \cr} \)
Cách khác:
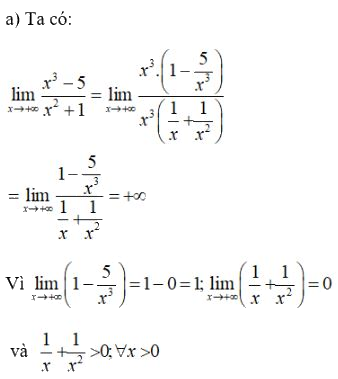
\(\mathop {\lim }\limits_{x \to - \infty } {{\sqrt {{x^4} - x} } \over {1 - 2x}}\)
Lời giải chi tiết:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^4} - x} }}{{1 - 2x}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^4}\left( {1 - \frac{1}{{{x^3}}}} \right)} }}{{1 - 2x}}\\ = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2}\sqrt {1 - \frac{1}{{{x^3}}}} }}{{x\left( {\frac{1}{x} - 2} \right)}} = \mathop {\lim }\limits_{x \to - \infty } \left[ {x.\frac{{\sqrt {1 - \frac{1}{{{x^3}}}} }}{{\frac{1}{x} - 2}}} \right]\end{array}\)
Ta có
\(\begin{array}{l}\mathop {\lim }\limits_{x \to - \infty } x = - \infty \\\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {1 - \frac{1}{{{x^3}}}} }}{{\frac{1}{x} - 2}} = \frac{1}{{ - 2}} < 0\end{array}\)
Do đó \(\mathop {\lim }\limits_{x \to - \infty } \left( {x.\frac{{\sqrt {1 - \frac{1}{{{x^3}}}} }}{{\frac{1}{x} - 2}}} \right) = + \infty \)
Vậy \(\mathop {\lim }\limits_{x \to - \infty } {{\sqrt {{x^4} - x} } \over {1 - 2x}}= + \infty \)
Cách khác:
Với mọi \(x < 0\), ta có \({{\sqrt {{x^4} - x} } \over {1 - 2x}} = {{{x^2}\sqrt {1 - {1 \over {{x^3}}}} } \over {1 - 2x}} = {{\sqrt {1 - {1 \over {{x^3}}}} } \over {{1 \over {{x^2}}} - {2 \over x}}}\)
Vì \(\mathop {\lim }\limits_{x \to - \infty } \sqrt {1 - {1 \over {{x^3}}}} = 1,\) \(\mathop {\lim }\limits_{x \to - \infty } \left( {{1 \over {{x^2}}} - {2 \over x}} \right) = 0\,\text{ và }\,{1 \over {{x^2}}} - {2 \over x} > 0\) với mọi \(x < 0\)
Nên \(\mathop {\lim }\limits_{x \to - \infty } {{\sqrt {{x^4} - x} } \over {1 - 2x}} = + \infty \)
Câu 36 trang 163 SGK Đại số và Giải tích 11 Nâng cao thuộc chương trình học lớp 11, tập trung vào việc ứng dụng đạo hàm để khảo sát hàm số. Bài toán này thường yêu cầu học sinh xác định các điểm cực trị, khoảng đồng biến, nghịch biến và vẽ đồ thị hàm số. Việc nắm vững kiến thức về đạo hàm và các quy tắc tính đạo hàm là yếu tố then chốt để giải quyết bài tập này một cách hiệu quả.
Trước khi đi vào giải chi tiết, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu. Thông thường, đề bài sẽ cung cấp một hàm số cụ thể và yêu cầu:
Để giải quyết bài toán này, chúng ta sẽ áp dụng các bước sau:
Giả sử hàm số được cho là: y = x3 - 3x2 + 2
Bước 1: Tập xác định: D = R
Bước 2: Đạo hàm bậc nhất: y' = 3x2 - 6x
Bước 3: Tìm điểm cực trị: 3x2 - 6x = 0 => x = 0 hoặc x = 2
- Tại x = 0, y' đổi dấu từ dương sang âm => x = 0 là điểm cực đại. y(0) = 2
- Tại x = 2, y' đổi dấu từ âm sang dương => x = 2 là điểm cực tiểu. y(2) = -2
Bước 4: Đạo hàm bậc hai: y'' = 6x - 6
Bước 5: Xác định khoảng lồi và lõm:
- y'' > 0 => 6x - 6 > 0 => x > 1 (khoảng lồi)
- y'' < 0 => 6x - 6 < 0 => x < 1 (khoảng lõm)
Bước 6: Điểm uốn: 6x - 6 = 0 => x = 1. y(1) = 0. Vậy điểm uốn là (1, 0)
Bước 7: Khoảng đồng biến và nghịch biến:
- y' > 0 => 3x2 - 6x > 0 => x < 0 hoặc x > 2 (đồng biến)
- y' < 0 => 3x2 - 6x < 0 => 0 < x < 2 (nghịch biến)
Khi giải các bài toán về khảo sát hàm số, cần chú ý đến các điểm sau:
Câu 36 trang 163 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải quyết các bài toán về khảo sát hàm số. Bằng cách áp dụng các phương pháp giải và lưu ý các điểm quan trọng, bạn có thể tự tin giải quyết bài tập này một cách hiệu quả.