Bài toán này thường yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ, và các tính chất hình học để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Cho hình chóp S.ABCD có SA ⊥ mp(ABC), các tam giác ABC và SBC không vuông. Gọi H và K lần lượt là trực tâm của tam giác ABC và SBC. Chứng minh rằng :
Đề bài
Cho hình chóp S.ABCD có SA ⊥ mp(ABC), các tam giác ABC và SBC không vuông. Gọi H và K lần lượt là trực tâm của tam giác ABC và SBC.
Chứng minh rằng :
a. AH, SK, BC đồng quy ;
b. SC ⊥ mp(BHK)
c. HK ⊥ mp(SBC).
Lời giải chi tiết
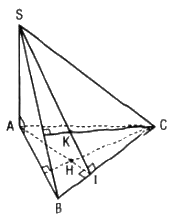
a. Gọi I là giao điểm của hai đường thẳng AH và BC
Ta có : BC ⊥ AH (do H là trực tâm ΔABC)
BC ⊥ SA (do SA ⊥ mp(ABC))
Suy ra BC ⊥ (SAI) mà SI ⊂ (SAI) nên BC ⊥ SI
K là trực tâm ΔSBC nên SI qua K
Vậy AH, SK, BC đồng quy tại I.
b. Ta có : BH ⊥ AC và BH ⊥ SA nên BH ⊥ mp(SAC)
Suy ra BH ⊥ SC
Mặt khác SC ⊥ BK nên SC ⊥ mp(BHK)
c. Ta có: SC ⊥ HK (do HK ⊥ mp(BHK)) mà HK ⊥ BC (do BC ⊥ mp(ASI))
Vậy HK ⊥ mp(SBC)
Bài toán Câu 18 trang 103 SGK Hình học 11 Nâng cao thường thuộc dạng bài tập về vectơ trong không gian, cụ thể là các bài toán liên quan đến chứng minh đẳng thức vectơ, tìm mối quan hệ giữa các vectơ, hoặc xác định vị trí tương đối của các điểm trong không gian.
(Đề bài cụ thể sẽ được chèn vào đây. Ví dụ: Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng: overrightarrow{AB} + vecd{AD} + vecd{AA'} = vecd{AC'})
Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức sau:
Phương pháp giải thường được sử dụng là:
(Lời giải chi tiết sẽ được trình bày ở đây, bao gồm các bước biến đổi vectơ, giải thích rõ ràng từng bước, và kết luận.)
Ví dụ (giả sử đề bài là chứng minh overrightarrow{AB} + vecd{AD} + vecd{AA'} = vecd{AC'}):
Ta có: overrightarrow{AC'} = vecd{AB} + vecd{BC'} = vecd{AB} + vecd{AD} + vecd{DC'} = vecd{AB} + vecd{AD} + vecd{AA'}
Vậy, overrightarrow{AB} + vecd{AD} + vecd{AA'} = vecd{AC'}.
Ngoài bài toán Câu 18 trang 103, còn rất nhiều bài tập tương tự về vectơ trong không gian. Các bài tập này thường yêu cầu học sinh:
Để nâng cao kiến thức và kỹ năng giải toán, học sinh nên luyện tập thêm các bài tập tương tự và tìm hiểu các phương pháp giải khác nhau.
Khi giải các bài toán về vectơ, học sinh nên:
Hy vọng với lời giải chi tiết và hướng dẫn giải trên, các bạn học sinh có thể tự tin giải quyết bài toán Câu 18 trang 103 SGK Hình học 11 Nâng cao và các bài tập tương tự. Chúc các bạn học tốt!
| Khái niệm | Giải thích |
|---|---|
| Vectơ | Một đoạn thẳng có hướng. |
| Phép cộng vectơ | Quy tắc hình bình hành hoặc quy tắc tam giác. |