Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho mặt phẳng (P) và ba điểm không thẳng hàng A, B, C cùng nằm ngoài (P). Chứng minh rằng nếu ba đường thẳng AB, BC, CA đều cắt mp (P) thì các giao điểm đó thẳng hàng
Đề bài
Cho mặt phẳng (P) và ba điểm không thẳng hàng A, B, C cùng nằm ngoài (P). Chứng minh rằng nếu ba đường thẳng AB, BC, CA đều cắt mp (P) thì các giao điểm đó thẳng hàng.
Lời giải chi tiết
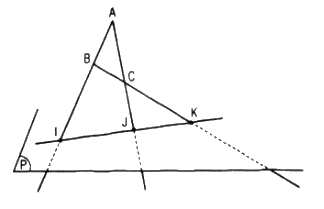
Gọi I, J, K lần lượt là giao điểm của AB, AC, BC với mp(P). A, B, C không thẳng hàng nên có mp(ABC).
Ta có:
\(\begin{array}{l}I = AB \cap \left( P \right)\\ \Rightarrow \left\{ \begin{array}{l}I \in AB \subset \left( {ABC} \right)\\I \in \left( P \right)\end{array} \right.\\ \Rightarrow I \in \left( {ABC} \right) \cap \left( P \right)\,\,\,\left( 1 \right)\\J = AC \cap \left( P \right)\\ \Rightarrow \left\{ \begin{array}{l}J \in AC \subset \left( {ABC} \right)\\J \in \left( P \right)\end{array} \right.\\ \Rightarrow J \in \left( {ABC} \right) \cap \left( P \right)\,\,\,\left( 2 \right)\end{array}\)
Từ (1) và (2)\( \Rightarrow \left( {ABC} \right) \cap \left( P \right) = IJ\)
Lại có,
\(\begin{array}{l}K = BC \cap \left( P \right)\\ \Rightarrow \left\{ \begin{array}{l}K \in BC \subset \left( {ABC} \right)\\K \in \left( P \right)\end{array} \right.\\ \Rightarrow K \in \left( {ABC} \right) \cap \left( P \right) = IJ\end{array}\)
Vậy I, J, K thẳng hàng.
Bài tập 5 trang 50 SGK Hình học 11 Nâng cao thường xoay quanh việc sử dụng các tính chất của vectơ, đặc biệt là các phép toán cộng, trừ, nhân với một số thực và tích vô hướng. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững định nghĩa vectơ, các quy tắc phép toán và các công thức liên quan.
Trước khi đi vào giải chi tiết, chúng ta cùng ôn lại một số kiến thức nền tảng:
Để giải quyết bài tập này, bước đầu tiên là đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Thông thường, đề bài sẽ cung cấp thông tin về các điểm, vectơ hoặc các mối quan hệ giữa chúng. Sau đó, cần vẽ hình minh họa để trực quan hóa bài toán và tìm ra hướng giải quyết.
Giả sử đề bài: Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng: 2MA2 + AB2 + AC2 = 3BC2
Lời giải:
Các bài tập tương tự thường yêu cầu chứng minh các đẳng thức liên quan đến vectơ, sử dụng các tính chất của trung điểm, trọng tâm, đường trung bình của tam giác. Mẹo giải là:
Để củng cố kiến thức, bạn nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Việc giải nhiều bài tập sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Hy vọng với lời giải chi tiết và hướng dẫn này, bạn đã hiểu rõ cách giải Câu 5 trang 50 SGK Hình học 11 Nâng cao. Chúc bạn học tốt!