Bài tập Câu 14 trang 18 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học Hình học 11. Bài toán này thường yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ, và các tính chất hình học cơ bản để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, cùng với phương pháp giải khoa học, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Giả sử phép đối xứng tâm
Nếu d không đi qua tâm đối xứng O thì d' song song với d, O cách đều d và d'
Lời giải chi tiết:
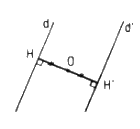
Kẻ \(OH ⊥ d (H ∈ d)\) thì vì d không đi qua O nên H không trùng với O
Phép đối xứng tâm \(Đ_ O\) biến H thành H’ thì O là trung điểm của HH’, và biến đường thẳng d thành đường thẳng d’ vuông góc với OH’ tại H’.
Suy ra d và d’ song song, cách đều điểm O
Hai đường thẳng d và d' trùng nhau khi và chỉ khi d đi qua O
Lời giải chi tiết:
Nếu d không đi qua điểm O thì theo câu a), d’ // d nên d’ không trùng với d.
Nếu d đi qua O thì mọi điểm \(M ∈ d\) biến thành điểm \(M’ ∈ d’.\)
Câu 14 trang 18 SGK Hình học 11 Nâng cao thường xoay quanh việc chứng minh đẳng thức vectơ, xác định mối quan hệ giữa các điểm trong không gian, hoặc tính toán các yếu tố hình học dựa trên vectơ. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản sau:
Để minh họa, giả sử đề bài yêu cầu chứng minh rằng với tam giác ABC, nếu G là trọng tâm thì GA + GB + GC = 0. Lời giải sẽ như sau:
Để giải các bài toán vectơ khác, bạn có thể áp dụng các phương pháp sau:
Xét bài toán: Cho hình vuông ABCD có cạnh a. Tính độ dài của vectơ AC.
Lời giải:
Để củng cố kiến thức, bạn nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Hãy chú trọng vào việc hiểu bản chất của bài toán và áp dụng các phương pháp giải một cách linh hoạt.
Câu 14 trang 18 SGK Hình học 11 Nâng cao là một bài toán quan trọng giúp học sinh rèn luyện kỹ năng giải toán vectơ và ứng dụng kiến thức vào thực tế. Bằng cách nắm vững các kiến thức cơ bản, áp dụng các phương pháp giải phù hợp, và luyện tập thường xuyên, bạn sẽ có thể tự tin giải quyết mọi bài toán về vectơ.