Bài tập này thường yêu cầu học sinh vận dụng kiến thức về vectơ, phương trình đường thẳng và các khái niệm liên quan đến hình học không gian để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác ABC nội tiếp trong đường tròn (O)
Đề bài
Cho tam giác ABC nội tiếp trong đường tròn (O) và một điểm M thay đổi trên (O). Gọi M1 là điểm đối xứng với M qua A, M2 là điểm đối xứng với M1 qua B, M3 là điểm đối xứng với M2 qua C
a. Chứng tỏ rằng phép biến hình F biến điểm M thành M3 là một phép đối xứng tâm
b. Tìm quỹ tích điểm M3
Lời giải chi tiết
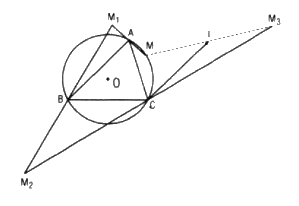
a. Gọi I là trung điểm của MM3, ta chứng minh I là điểm cố định
Thật vậy, ta có:
\(\eqalign{& \overrightarrow {CI} = {1 \over 2}\left( {\overrightarrow {CM} + \overrightarrow {C{M_3}} } \right) \cr & \,\,\,\,\,\,\, = {1 \over 2}\left( {\overrightarrow {CM} + \overrightarrow {{M_2}C} } \right) \cr & \,\,\,\,\,\,\, = {1 \over 2}\overrightarrow {{M_2}M} = \overrightarrow {BA} \cr} \)
Như vậy điểm I cố định, do đó phép biến hình F biến M thành M3 là phép đối xứng qua điểm I
b. Quỹ tích điểm M3 là đường tròn (O’), ảnh của đường tròn (O) qua phép đối xứng tâm với tâm I
Câu 5 trang 34 SGK Hình học 11 Nâng cao thường xoay quanh các bài toán liên quan đến vectơ, đặc biệt là các bài toán chứng minh đẳng thức vectơ, tìm mối quan hệ giữa các vectơ, hoặc xác định vị trí tương đối của các điểm trong không gian.
Trước khi đi vào giải chi tiết, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:
Để giải quyết Câu 5 trang 34, bước đầu tiên là đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Thường thì đề bài sẽ cung cấp thông tin về các điểm, vectơ, hoặc các mối quan hệ giữa chúng. Việc phân tích đề bài chính xác sẽ giúp chúng ta lựa chọn phương pháp giải phù hợp.
(Giả sử đề bài Câu 5 trang 34 là: Cho bốn điểm A, B, C, D không đồng phẳng. Chứng minh rằng: overrightarrow{AB} + vecd{AC} + vecd{AD} = 3overrightarrow{AG} với G là trọng tâm của tam giác BCD.)
Lời giải:
Ngoài bài toán trên, Câu 5 trang 34 có thể xuất hiện các dạng bài tập tương tự như:
Để giải tốt các bài tập về vectơ, bạn nên:
Hy vọng với lời giải chi tiết và các lưu ý trên, bạn sẽ tự tin giải quyết Câu 5 trang 34 SGK Hình học 11 Nâng cao và các bài tập tương tự. Chúc bạn học tốt!