Cho hình bình hành ABCD nằm trong mặt phẳng (P) và một điểm S nằm ngoài mp(P). Gọi M là điểm nằm giữa S và A ; N là điểm giữa S và B; giao điểm của hai đường thẳng AC và BD là O
Đề bài
Cho hình bình hành ABCD nằm trong mặt phẳng (P) và một điểm S nằm ngoài mp(P). Gọi M là điểm nằm giữa S và A ; N là điểm giữa S và B; giao điểm của hai đường thẳng AC và BD là O
a. Tìm giao điểm của mặt phẳng (CMN) với đường thẳng SO
b. Xác định giao tuyến của hai mặt phẳng (SAD) và (CMN)
Lời giải chi tiết
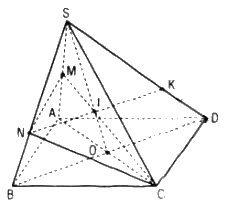
a. Tìm SO ∩ (CNM)
Trong mặt phẳng (SAC) gọi I là giao điểm của SO với CM
I = SO ∩ CM
\( \Rightarrow \left\{ \begin{array}{l}I \in SO\\I \in CM\end{array} \right.\)
mà CM ⊂ (CMN) nên I = SO ∩ (CMN)
b. Tìm (SAD) ∩ (CMN)
Trong mp(SBD) gọi K là giao điểm của NI và SD
K = NI ∩ SD
\( \Rightarrow \left\{ \begin{array}{l}K \in NI \subset \left( {CMN} \right)\\K \in SD \subset \left( {SAD} \right)\end{array} \right. \)\(\Rightarrow K \in \left( {CMN} \right) \cap \left( {SAD} \right)\)
Mà \(M \in \left( {SAD} \right) \cap \left( {CMN} \right)\)
Do đó (SAD) ∩ (CMN) = MK
