Bài toán này thường yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ, và ứng dụng vào hình học không gian để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững phương pháp giải và tự tin làm bài tập.
Cho hình chóp S.ABCD có đáy là hình chữ nhật và Ab = 2a, BC = a. Các cạnh bên của hình chóp bằng nhau và bằng
Đề bài
Cho hình chóp S.ABCD có đáy là hình chữ nhật và AB = 2a, BC = a. Các cạnh bên của hình chóp bằng nhau và bằng \(a\sqrt 2 \)
a. Tính khoảng cách từ S đến mặt phẳng đáy (ABCD).
b. Gọi E và F lần lượt là trung điểm các cạnh AB và CD ; K là điểm bất kì thuộc đường thẳng AD. Chứng minh rằng khoảng cách giữa hai đường thẳng EF và SK không phụ thuộc vào K, hãy tính khoảng cách đó theo a.
Lời giải chi tiết
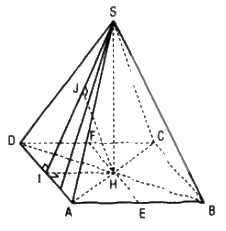
a. Gọi H là hình chiếu của S lên (ABCD).
Khi đó \(SH \bot \left( {ABCD} \right)\).
Xét các tam giác SHA, SHB, SHC, SHD có:
\(\widehat {SHA} = \widehat {SHB} = \widehat {SHC} = \widehat {SHD} = {90^0}\) (vì \(SH \bot \left( {ABCD} \right)\)
Chung SH
Nên \(\Delta SHA = \Delta SHB = \Delta SHC = \Delta SHD\) (2 cạnh góc vuông)
\( \Rightarrow HA = HB = HC = HD\)
\( \Rightarrow H\) là tâm đường tròn ngoại tiếp hình chữ nhật ABCD.
\( \Rightarrow H\) là giao điểm của AC và BD.
Ta có:
\(\eqalign{ & S{H^2} = S{A^2} - A{H^2} \cr&= S{A^2} - {\left( {\frac{{AC}}{2}} \right)^2}= S{A^2} - {{A{C^2}} \over 4} \cr&= 2{a^2} - {{A{B^2} + B{C^2}} \over 4} \cr & = 2{a^2} - {{4{a^2} + {a^2}} \over 4} = {{3{a^2}} \over 4}\cr&\Rightarrow SH = {{a\sqrt 3 } \over 2} \cr} \)
Cách khác:

b. Vì EF // AD nên EF // mp(SAD), mặt khác SK nằm trong mp(SAD) nên khoảng cách giữa EF và SK chính là khoảng cách giữa EF và mp(SAD), đó cũng chính là khoảng cách từ H đến mp(SAD).
Vậy khoảng cách giữa EF và SK không phụ thuộc vào vị trí của điểm K trên đường thẳng AD.
Tính d(EF ; SK) :
Gọi I là trung điểm của AD
\( \Rightarrow HI \bot AD\)
Mà \(AD \bot SH\) (do \(SH \bot \left( {ABCD} \right)\)
Nên \(AD \bot \left( {SHI} \right)\).
Kẻ đường cao HJ của tam giác vuông SHI thì
\(\left\{ \begin{array}{l}HJ \bot SI\\HJ \bot AD\left( {AD \bot \left( {SHI} \right)} \right)\end{array} \right.\)\( \Rightarrow HJ \bot \left( {SAD} \right)\)
Do đó d(H; (SAD)) = HJ.
Ta có: HJ.SI = SH.HI
\(S{I^2} = S{A^2} - A{I^2} = 2{a^2} - {{{a^2}} \over 4} = {{7{a^2}} \over 4}\)
Từ đó \(HJ = {{SH.HI} \over {SI}} = {{{{a\sqrt 3 } \over 2}.a} \over {{{a\sqrt 7 } \over 2}}} = {{a\sqrt {21} } \over 7}\)
Như vậy, khoảng cách giữa EF và SK không phụ thuộc vào vị trí của điểm K trên đường thẳng AD và bằng \({{a\sqrt {21} } \over 7}\)
Câu 34 trang 118 SGK Hình học 11 Nâng cao thường liên quan đến việc xác định mối quan hệ giữa các vectơ trong không gian, tính toán độ dài vectơ, tích vô hướng, và ứng dụng vào việc chứng minh các tính chất hình học.
Trước khi bắt đầu giải, điều quan trọng là phải đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Phân tích đề bài giúp ta định hướng phương pháp giải phù hợp.
Để giải quyết bài toán này, bạn cần nắm vững các kiến thức sau:
Có nhiều phương pháp giải khác nhau tùy thuộc vào từng dạng bài cụ thể. Một số phương pháp thường được sử dụng:
(Ở đây sẽ là lời giải chi tiết của câu 34 trang 118 SGK Hình học 11 Nâng cao. Lời giải này sẽ bao gồm các bước giải cụ thể, giải thích rõ ràng, và sử dụng các công thức, định lý liên quan. Ví dụ, nếu đề bài yêu cầu chứng minh một đẳng thức vectơ, lời giải sẽ trình bày các bước biến đổi để chứng minh đẳng thức đó.)
Để giúp bạn hiểu rõ hơn về phương pháp giải, chúng ta sẽ xem xét một ví dụ minh họa:
(Ở đây sẽ là một ví dụ tương tự câu 34 trang 118, được giải chi tiết để người đọc có thể tham khảo và áp dụng vào các bài toán khác.)
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự sau:
Khi giải các bài toán về vectơ, bạn cần chú ý:
Câu 34 trang 118 SGK Hình học 11 Nâng cao là một bài toán quan trọng giúp bạn rèn luyện kỹ năng giải toán về vectơ và ứng dụng vào hình học không gian. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, bạn đã nắm vững phương pháp giải và tự tin làm bài tập.
| Khái niệm | Giải thích |
|---|---|
| Vectơ | Một đoạn thẳng có hướng. |
| Tích vô hướng | Một phép toán giữa hai vectơ cho ra một số. |