Bài toán này thường yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ, và các tính chất hình học để giải quyết.
giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải toán.
Cho tứ diện ABCD. Các điểm P, Q lần lượt là trung điểm của AB và CD; điểm R nằm trên cạnh BC sao cho BR = 2RC. Gọi S là giao điểm của mp(PQR) và cạnh AD. Chứng minh rằng AS = 2SD
Đề bài
Cho tứ diện ABCD. Các điểm P, Q lần lượt là trung điểm của AB và CD; điểm R nằm trên cạnh BC sao cho BR = 2RC. Gọi S là giao điểm của mp(PQR) và cạnh AD. Chứng minh rằng AS = 2SD.
Phương pháp giải - Xem chi tiết
Áp dụng định lí Menelaus để giải bài toán
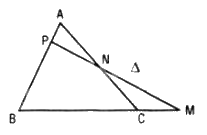
Giả sử đường thẳng Δ cắt các cạnh (hoặc phần kéo dài) BC, CA, AB lần lượt tại M, N, P thì :
\({{MB} \over {MC}}.{{NC} \over {NA}}.{{PA} \over {PB}} = 1\)
Lời giải chi tiết
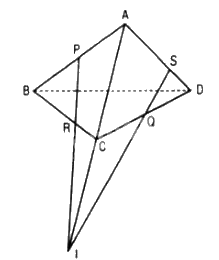
Trong (ABC), gọi {I} = PR ∩ AC
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}\left( {PQR} \right) \cap \left( {ABC} \right) = PR\\\left( {ABC} \right) \cap \left( {ACD} \right) = AC\\\left( {PQR} \right) \cap \left( {ACD} \right) = Qt\\AC \cap PR = I\end{array} \right.\\ \Rightarrow I \in Qt\end{array}\)
Trong mp(ACD) gọi {S} = QI ∩ AD
Thì {S} = AD ∩ (PQR)
Áp dụng định lí Menelaus trong tam giác ABC với cát tuyến PRI ta có
\({{PA} \over {PB}}.{{RB} \over {RC}}.{{IC} \over {IA}} = 1 \)\(\Rightarrow 1.2.{{IC} \over {IA}} = 1\)
\( \Rightarrow {{IC} \over {IA}} = {1 \over 2}\) ⇒ C là trung điểm của AI.
Áp dụng định lí Menelaus trong tam giác ACD với cát tuyến IQS ta có :
\({{IC} \over {IA}}.{{SA} \over {SD}}.{{QD} \over {QC}} = 1 \Rightarrow {1 \over 2}.{{SA} \over {SD}}.1 = 1 \)
\(\Rightarrow SA = 2SD\,\,\left( {dpcm} \right)\)
Câu 21 trang 55 SGK Hình học 11 Nâng cao thường thuộc chương trình học về vectơ trong không gian. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Trước khi bắt tay vào giải, học sinh cần đọc kỹ đề bài, xác định rõ yêu cầu của bài toán. Thông thường, bài toán sẽ cho trước một số vectơ hoặc các yếu tố hình học liên quan. Nhiệm vụ của học sinh là:
Đề bài (giả định): Cho hình hộp ABCD.A'B'C'D'. Gọi M là trung điểm của cạnh AB. Chứng minh rằng vectơ MM' vuông góc với mặt phẳng (ABCD).
Lời giải:
Ngoài câu 21 trang 55, học sinh có thể gặp các dạng bài tập tương tự, bao gồm:
Để giải tốt các bài tập về vectơ, học sinh nên:
Học sinh có thể tham khảo thêm các tài liệu sau để học tốt môn Hình học:
Câu 21 trang 55 SGK Hình học 11 Nâng cao là một bài toán điển hình về ứng dụng của vectơ trong không gian. Việc nắm vững kiến thức và kỹ năng giải toán vectơ là rất quan trọng để học tốt môn Hình học. giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và các hướng dẫn trên, học sinh sẽ tự tin giải quyết bài toán này và các bài toán tương tự.