Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Hình học 11 Nâng cao. Bài viết này sẽ hướng dẫn bạn giải quyết Câu 17 trang 19 SGK Hình học 11 Nâng cao một cách dễ hiểu nhất.
Chúng tôi luôn cố gắng mang đến những giải pháp tối ưu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho hai điểm cố định trên đường tròn
Đề bài
Cho hai điểm cố định B, C trên đường tròn \((O; R)\) và một điểm A thay đổi trên đường tròn đó. Hãy dùng phép đối xứng tâm để chứng minh rằng trực tâm H của tam giác ABC nằm trên một đường tròn cố định
Hướng dẫn. Gọi I là trung điểm BC . Hãy vẽ đường kính AM của đường tròn rồi chứng minh rằng I là trung điểm của đoạn thẳng HM
Lời giải chi tiết
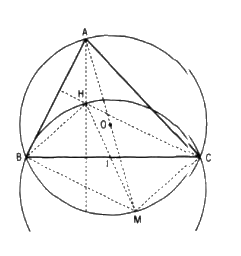
Nếu BC là đường kính thì tam giác ABC vuông tại A, do đó H trùng A nằm trên (O;R) cố định.
Nếu BC không là đường kính thì vẽ đường kính AM của đường tròn.
Khi đó,
BH // MC (vì cùng vuông góc với AC)
CH // MB (vì cùng vuông góc với AB)
Do đó BHCM là hình bình hành nên BC và MH cắt nhau tại trùng điểm I của mỗi đường.
Hay I là trung điểm của MH.
Vậy phép đối xứng qua điểm I biến M thành H.
Khi A chạy trên đường tròn \((O ; R)\) thì M chạy trên đường tròn \((O ; R)\).
Do đó, H nằm trên đường tròn là ảnh của đường tròn \((O ; R)\) qua phép đối xứng tâm I.
Câu 17 trang 19 SGK Hình học 11 Nâng cao thường xoay quanh các kiến thức về vectơ, đặc biệt là các phép toán vectơ và ứng dụng trong hình học không gian. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản như:
Để cung cấp một lời giải cụ thể, chúng ta cần biết nội dung chính xác của Câu 17 trang 19. Tuy nhiên, dựa trên kinh nghiệm giải các bài tập tương tự, chúng ta có thể đưa ra một phương pháp tiếp cận chung:
Giả sử Câu 17 yêu cầu chứng minh hai vectơ vuông góc.
Để chứng minh hai vectơ a và b vuông góc, chúng ta cần chứng minh tích vô hướng của chúng bằng 0: a ⋅ b = 0.
Nếu a = (x1, y1, z1) và b = (x2, y2, z2), thì a ⋅ b = x1x2 + y1y2 + z1z2.
Chúng ta sẽ tính tích vô hướng này và nếu kết quả bằng 0, thì hai vectơ đó vuông góc.
Ngoài Câu 17, SGK Hình học 11 Nâng cao còn có nhiều bài tập khác liên quan đến vectơ và hình học không gian. Một số dạng bài tập thường gặp bao gồm:
Để học tốt Hình học 11 Nâng cao, bạn nên:
Câu 17 trang 19 SGK Hình học 11 Nâng cao là một bài tập quan trọng giúp bạn củng cố kiến thức về vectơ và hình học không gian. Hy vọng rằng với lời giải chi tiết và phương pháp tiếp cận chung mà chúng tôi đã trình bày, bạn sẽ tự tin hơn trong việc giải quyết bài toán này và các bài tập tương tự.