Giải Câu 4 Trang 120 SGK Hình học 11 Nâng cao

Câu 4 trang 120 SGK Hình học 11 Nâng cao

Câu 4 trang 120 SGK Hình học 11 Nâng cao là một bài tập quan trọng trong chương trình Hình học 11 Nâng cao.

Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.

Tam giác ABC vuông có cạnh huyền BC nằm trong mp(P), cạnh AB và AC lần lượt tạo với mp(P) các góc β và γ. Gọi α là góc tạo bởi mp(P) và mp(ABC). Chứng minh rằng

Đề bài

Tam giác ABC vuông có cạnh huyền BC nằm trong mp(P), cạnh AB và AC lần lượt tạo với mp(P) các góc β và γ. Gọi α là góc tạo bởi mp(P) và mp(ABC). Chứng minh rằng \({\sin ^2}\alpha = {\sin ^2}\beta + {\sin ^2}\gamma \)

Phương pháp giải - Xem chi tiết Câu 4 trang 120 SGK Hình học 11 Nâng cao 1

Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.

Lời giải chi tiết

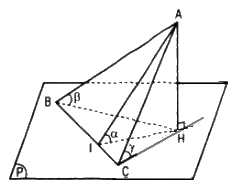
Câu 4 trang 120 SGK Hình học 11 Nâng cao 2

Kẻ AH ⊥ mp(P) và AI ⊥ BC.

Khi đó HB là hình chiếu của AB trên (P) nên góc giữa AB và (P) bằng góc giữa AB và HB hay \(\beta = \widehat {ABH}\)

HC là hình chiếu của AC trên (P) nên góc giữa AC và (P) bằng góc giữa AC và HC hay \(\gamma = \widehat {ACH}\)

Lại có:

\(\left\{ \begin{array}{l}AI \bot BC\\AH \bot BC\left( {AH \bot \left( P \right)} \right)\end{array} \right. \) \(\Rightarrow BC \bot \left( {AIH} \right) \Rightarrow BC \bot HI\)

Mà \(BC \bot AI\) và \(\left( {ABC} \right) \cap \left( P \right) = BC\) nên góc giữa (ABC) và (P) bằng góc giữa AI và HI hay \(\alpha = \widehat {AIH}.\) (do \(\widehat {AIH}<90^0\)).

Vì ΔABC vuông ở A nên :

\(\eqalign{ & {1 \over {A{I^2}}} = {1 \over {A{B^2}}} + {1 \over {A{C^2}}} \cr & \Rightarrow {{A{H^2}} \over {A{I^2}}} = {{A{H^2}} \over {A{B^2}}} + {{A{H^2}} \over {A{C^2}}} \cr & hay\,\,{\sin ^2}\alpha = {\sin ^2}\beta + {\sin ^2}\gamma \cr} \)

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Câu 4 trang 120 SGK Hình học 11 Nâng cao – hành trang không thể thiếu trong chuyên mục toán 11 trên nền tảng môn toán. Bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải Chi Tiết Câu 4 Trang 120 SGK Hình Học 11 Nâng Cao

Câu 4 trang 120 SGK Hình học 11 Nâng cao thuộc chương trình học Hình học lớp 11, tập trung vào việc củng cố kiến thức về vectơ và ứng dụng của chúng trong giải quyết các bài toán hình học. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:

Vectơ: Định nghĩa, các phép toán cộng, trừ, nhân với một số thực.
Tích vô hướng của hai vectơ: Công thức tính, ứng dụng để tính góc giữa hai vectơ, kiểm tra vuông góc.
Hệ tọa độ: Biểu diễn vectơ trong hệ tọa độ, các phép toán vectơ trong hệ tọa độ.

Phân Tích Đề Bài

Trước khi bắt tay vào giải, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Thông thường, đề bài sẽ cung cấp một hình vẽ hoặc một mô tả về các điểm, đường thẳng, hoặc các yếu tố hình học khác. Nhiệm vụ của học sinh là sử dụng kiến thức đã học để tìm ra các đại lượng cần tính, chứng minh các mối quan hệ, hoặc giải quyết các vấn đề được đặt ra.

Lời Giải Chi Tiết

Để minh họa, giả sử đề bài yêu cầu:

Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng: 2MA² + AB² + AC² = 3BC²

Lời giải:

Sử dụng công thức trung điểm:MA = (AB + AC) / 2
Bình phương hai vế:4MA² = AB² + AC² + 2AB.AC
Biến đổi biểu thức:2MA² = (AB² + AC² + 2AB.AC) / 2
Sử dụng công thức trung tuyến:AB² + AC² = 2(AM² + BM²), với BM = BC / 2
Thay thế và rút gọn: Thay các biểu thức trên vào phương trình ban đầu, ta sẽ chứng minh được 2MA² + AB² + AC² = 3BC²

Các Dạng Bài Tập Tương Tự

Ngoài bài toán trên, còn rất nhiều dạng bài tập tương tự liên quan đến vectơ và ứng dụng trong hình học. Một số dạng bài tập phổ biến bao gồm:

Chứng minh đẳng thức vectơ.
Tìm tọa độ của một điểm hoặc vectơ.
Tính diện tích tam giác, tứ giác bằng vectơ.
Chứng minh các điểm thẳng hàng, song song, vuông góc.

Mẹo Giải Bài Tập

Để giải các bài tập về vectơ một cách hiệu quả, bạn có thể áp dụng một số mẹo sau:

Vẽ hình: Vẽ hình giúp bạn hình dung rõ hơn về bài toán và các yếu tố liên quan.
Chọn hệ tọa độ thích hợp: Việc chọn hệ tọa độ phù hợp có thể giúp đơn giản hóa bài toán.
Sử dụng các công thức: Nắm vững các công thức về vectơ và áp dụng chúng một cách linh hoạt.
Biến đổi đại số: Sử dụng các phép biến đổi đại số để rút gọn biểu thức và tìm ra kết quả.

Luyện Tập Thêm

Để củng cố kiến thức và kỹ năng giải bài tập, bạn nên luyện tập thêm với các bài tập khác trong SGK và các tài liệu tham khảo. Ngoài ra, bạn có thể tìm kiếm các bài giảng trực tuyến hoặc tham gia các khóa học luyện thi để được hướng dẫn chi tiết và giải đáp thắc mắc.

Kết Luận

Câu 4 trang 120 SGK Hình học 11 Nâng cao là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải quyết các bài toán hình học bằng vectơ. Bằng cách nắm vững kiến thức cơ bản, phân tích đề bài một cách cẩn thận, và áp dụng các mẹo giải bài tập, bạn có thể tự tin giải quyết bài toán này và các bài toán tương tự một cách hiệu quả.