Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin làm bài.
Hình 5.5 là đồ thị của hàm số y = f(x) xác
Đề bài
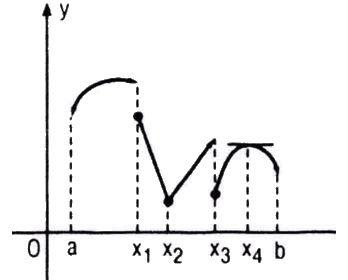
Hình 5.5 là đồ thị của hàm số y = f(x) xác định trên khoảng (a ; b). Dựa vào hình vẽ, hãy cho biết tại mỗi điểm x1, x2, x3 và x4 :
a. Hàm số có liên tục hay không ?
b. Hàm số có đạo hàm hay không ? Hãy tính đạo hàm nếu có.
Lời giải chi tiết
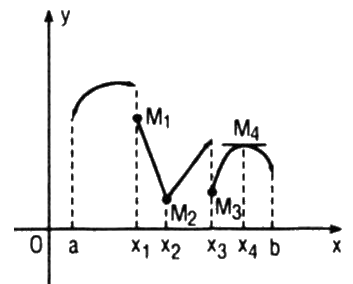
Căn cứ vào hình ta nhận thấy :
+ Hàm số đã cho gián đoạn tại các điểm x1 và x3; vì đồ thị hàm số bị ngắt quãng khi đi qua các điểm M1 và M3.
+ Hàm số đã cho liên tục tại các điểm x2 và x4; vì đồ thị hàm số là đường “liền nét” khi đi qua các điểm M2 và M4
+ Hàm số không có đạo hàm tại điểm x2; vì điểm M2 đồ thị là đường “gấp khúc” (và hiển nhiên tại đó không có tiếp tuyến của đồ thị hàm số), giống như đồ thị hàm số \(y = |x|\).
+ Hàm số có đạo hàm tại điểm M4 và \(f'\left( {{x_4}} \right) = 0;\) vì tại điểm M4 đồ thị của hàm số có tiếp tuyến và tiếp tuyến này song song với trục hoành.
Câu 15 trang 195 SGK Đại số và Giải tích 11 Nâng cao thuộc chương trình học lớp 11, tập trung vào việc ứng dụng đạo hàm để giải quyết các bài toán liên quan đến hàm số. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Trước khi bắt đầu giải bài toán, chúng ta cần phân tích đề bài một cách cẩn thận để xác định rõ yêu cầu và các thông tin đã cho. Thông thường, đề bài sẽ cung cấp một hàm số và yêu cầu tính đạo hàm của hàm số đó tại một điểm cụ thể hoặc tìm các điểm cực trị của hàm số. Đôi khi, đề bài cũng có thể yêu cầu sử dụng đạo hàm để giải quyết các bài toán thực tế, chẳng hạn như tìm vận tốc của một vật thể tại một thời điểm nhất định.
(Giả sử đề bài là: Cho hàm số y = x3 - 3x2 + 2. Tìm đạo hàm của hàm số và tìm các điểm cực trị.)
y' = 3x2 - 6x
Để tìm điểm cực trị, ta giải phương trình y' = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
Ta xét dấu của đạo hàm y' trên các khoảng xác định:
Vậy, hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 2.
y(0) = 2 (cực đại)
y(2) = -2 (cực tiểu)
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, bạn có thể tham khảo các bài tập tương tự trong SGK Đại số và Giải tích 11 Nâng cao hoặc trên các trang web học toán online khác. Việc luyện tập thường xuyên sẽ giúp bạn nắm vững kiến thức và tự tin hơn khi làm bài kiểm tra.
Câu 15 trang 195 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính đạo hàm và ứng dụng đạo hàm để giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và các lưu ý trên, bạn sẽ hiểu rõ hơn về bài toán này và tự tin hơn khi làm bài tập.