Chào mừng bạn đến với giaitoan.edu.vn! Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho Câu 22 trang 55 SGK Hình học 11 Nâng cao. Chúng tôi sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán Hình học một cách hiệu quả.
Gọi G là trọng tâm của tứ diện ABCD a. Chứng minh rằng đường thẳng đi qua G và một đỉnh của tứ diện sẽ đi qua trọng tâm của mặt đối diện với đỉnh ấy b. Gọi A’ là trọng tâm của mặt BCD. Chứng minh rằng GA = 3GA’
Đề bài
Gọi G là trọng tâm của tứ diện ABCD
a. Chứng minh rằng đường thẳng đi qua G và một đỉnh của tứ diện sẽ đi qua trọng tâm của mặt đối diện với đỉnh ấy
b. Gọi A’ là trọng tâm của mặt BCD. Chứng minh rằng GA = 3GA’
Phương pháp giải - Xem chi tiết
- G là trọng tâm tứ diện thì G là trung điểm của đoạn nối trung điểm hai cạnh đối của tứ diện.
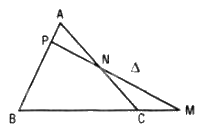
- Định lí Menelaus: Giả sử đường thẳng Δ cắt các cạnh (hoặc phần kéo dài) BC, CA, AB lần lượt tại M, N, P thì :
\({{MB} \over {MC}}.{{NC} \over {NA}}.{{PA} \over {PB}} = 1\)
Lời giải chi tiết
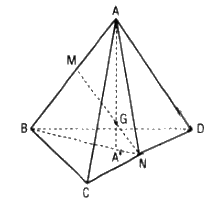
a. Gọi M, N là trung điểm của AB, CD.
G là trọng tâm tứ diện nên G là trung điểm của MN hay GM=GN.
Trong mp(ABN) gọi A’ là giao điểm của AG với trung tuyến BN của ΔBCD.
Ta chứng minh A' là trọng tâm tam giác BCD hay A’B = 2A’N.
Áp dụng định lí Menelaus trong ΔBMN với cát tuyến AGA’ ta có :
\({{AM} \over {AB}}.{{GN} \over {GM}}.{{A'B} \over {A'N}} = 1 \)\(\Rightarrow {1 \over 2}.1.{{A'B} \over {A'N}} = 1 \Rightarrow A'B = 2A'N\)
Vậy A’ là trọng tâm của ΔBCD
Tương tự BG ,CG, DG lần lượt đi qua trọng tâm B’, C’, D’ của tam giác ACD, ABD, ABC.
b. Chứng minh GA = 3GA’
Áp dụng định lí Menelaus trong ΔABA’ với cát tuyến MGN ta có :
\({{MA} \over {MB}}.{{GA'} \over {GA}}.{{NB} \over {NA'}} = 1 \)\(\Rightarrow 1.{{GA'} \over {GA}}.3 = 1 \)
\(\Rightarrow GA = 3GA'\,\,\left( {dpcm} \right)\)
Câu 22 trang 55 SGK Hình học 11 Nâng cao thường xoay quanh các kiến thức về vectơ, đặc biệt là các phép toán vectơ trong không gian. Bài tập này có thể yêu cầu học sinh chứng minh đẳng thức vectơ, tìm tọa độ của vectơ, hoặc xác định mối quan hệ giữa các vectơ.
Trước khi đi vào giải chi tiết, chúng ta cần ôn lại một số kiến thức cơ bản:
Để giải quyết Câu 22 trang 55, bước đầu tiên là đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Thông thường, đề bài sẽ cung cấp thông tin về các điểm trong không gian, các vectơ liên quan, hoặc các mối quan hệ giữa chúng. Sau đó, chúng ta cần xác định phương pháp giải phù hợp, dựa trên các kiến thức đã học.
(Giả sử đề bài là: Cho A(1;2;3), B(2;4;5), C(3;6;7). Chứng minh rằng A, B, C thẳng hàng.)
Lời giải:
Nếu tồn tại một số k sao cho AC = k.AB thì A, B, C thẳng hàng.
Trong trường hợp này, ta thấy AC = 2.AB, do đó A, B, C thẳng hàng.
Ngoài dạng bài chứng minh ba điểm thẳng hàng, Câu 22 trang 55 và các bài tập tương tự có thể xuất hiện dưới các dạng khác nhau:
Để giải các bài tập này, bạn cần nắm vững các kiến thức về vectơ, tọa độ vectơ, tích vô hướng, tích có hướng, và các ứng dụng của chúng. Ngoài ra, việc luyện tập thường xuyên với các bài tập khác nhau sẽ giúp bạn rèn luyện kỹ năng giải toán và làm quen với các dạng bài tập khác nhau.
Hình học 11 Nâng cao đòi hỏi sự tư duy logic và khả năng hình dung không gian tốt. Dưới đây là một số lời khuyên để giúp bạn học tốt môn học này:
Hy vọng bài giải chi tiết này sẽ giúp bạn hiểu rõ hơn về Câu 22 trang 55 SGK Hình học 11 Nâng cao và tự tin hơn trong việc giải các bài tập tương tự. Chúc bạn học tốt!