Bài toán này yêu cầu học sinh vận dụng kiến thức về hàm số, đạo hàm để giải quyết. Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập toán 11 nâng cao.
Gieo hai con súc sắc cân đối.
Mô tả không gian mẫu.
Phương pháp giải:
- Liệt kê các phần tử của không gian mẫu.
- Liệt kê các khả năng thuận lời cho từng biến cố A, B, C.
- Tính xác suất theo công thức \(P\left( A \right) = \dfrac{{\left| {{\Omega _A}} \right|}}{{\left| \Omega \right|}}\)
Lời giải chi tiết:
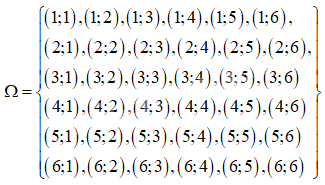
Không gian mẫu có 36 phần tử.
Gọi A là biến cố “Tổng số chấm trên mặt xuất hiện của hai con súc sắc nhỏ hơn hoặc bằng 7”. Liệt kê các kết quả thuận lợi cho A. Tính P(A).
Phương pháp giải:
- Liệt kê các phần tử của không gian mẫu.
- Liệt kê các khả năng thuận lời cho từng biến cố A, B, C.
- Tính xác suất theo công thức \(P\left( A \right) = \dfrac{{\left| {{\Omega _A}} \right|}}{{\left| \Omega \right|}}\)
Lời giải chi tiết:
Ta có:
\({\Omega _A} = \left\{ \begin{array}{l}\left( {1;1} \right),\left( {1;2} \right),\left( {1;3} \right),\left( {1;4} \right),\left( {1;5} \right),\left( {1;6} \right)\\\left( {2;1} \right),\left( {2;2} \right),\left( {2;3} \right),\left( {2;4} \right),\left( {2;5} \right),\\\left( {3;1} \right),\left( {3;2} \right),\left( {3;3} \right),\left( {3;4} \right),\left( {4;1} \right),\\\left( {4;2} \right),\left( {4;3} \right),\left( {5;1} \right),\left( {5;2} \right),\left( {6;1} \right)\end{array} \right\}\)
Tập \({\Omega _A}\) có \(21\) phần tử.
Vậy \(\displaystyle P\left( A\right) = {{21} \over {36}}= {{7} \over {12}}\).
Cũng hỏi như trên cho các biến cố B : “Có ít nhất một con súc sắc xuất hiện mặt 6 chấm” và C “Có đúng một con súc sắc xuất hiện mặt 6 chấm”.
Phương pháp giải:
- Liệt kê các phần tử của không gian mẫu.
- Liệt kê các khả năng thuận lời cho từng biến cố A, B, C.
- Tính xác suất theo công thức \(P\left( A \right) = \dfrac{{\left| {{\Omega _A}} \right|}}{{\left| \Omega \right|}}\)
Lời giải chi tiết:
\({\Omega _B} = \left\{ \begin{array}{l}\left( {6;1} \right),\left( {6;2} \right),\left( {6;3} \right),\left( {6;4} \right),\\\left( {6;5} \right),\left( {6;6} \right),\left( {1;6} \right),\left( {2;6} \right),\\\left( {3;6} \right),\left( {4;6} \right),\left( {5;6} \right)\end{array} \right\}\)
Tập \({\Omega _B}\) có \(11\) phần tử.
Vậy \(\displaystyle P\left( B\right) = {{11} \over {36}}\).
\({\Omega _C} = \left\{ \begin{array}{l}\left( {6;1} \right),\left( {6;2} \right),\left( {6;3} \right),\left( {6;4} \right),\left( {6;5} \right),\\\left( {1;6} \right),\left( {2;6} \right),\left( {3;6} \right),\left( {4;6} \right),\left( {5;6} \right)\end{array} \right\}\)
Vậy \({\Omega _C}\)có \(10\) phần tử.
Do đó \(\displaystyle P\left( C \right) = {{10} \over {36}} = {5 \over {18}}.\)
Câu 28 trang 76 SGK Đại số và Giải tích 11 Nâng cao thuộc chương trình học kỳ I, lớp 11, tập trung vào việc ứng dụng đạo hàm để khảo sát hàm số. Bài toán này thường yêu cầu học sinh xác định các điểm cực trị, khoảng đồng biến, nghịch biến và vẽ đồ thị hàm số. Việc nắm vững kiến thức về đạo hàm và các quy tắc tính đạo hàm là yếu tố then chốt để giải quyết bài toán này một cách hiệu quả.
Thông thường, câu 28 trang 76 sẽ đưa ra một hàm số cụ thể, ví dụ như một hàm đa thức bậc ba hoặc một hàm phân thức. Yêu cầu của bài toán có thể bao gồm:
Để giải quyết bài toán này, học sinh cần thực hiện theo các bước sau:
Giả sử hàm số cho là: y = x3 - 3x2 + 2
Bước 1: Tập xác định: D = R
Bước 2: Đạo hàm: y' = 3x2 - 6x; y'' = 6x - 6
Bước 3: Tìm điểm cực trị: 3x2 - 6x = 0 => x = 0 hoặc x = 2. Tại x = 0, y' đổi dấu từ dương sang âm => x = 0 là điểm cực đại. Tại x = 2, y' đổi dấu từ âm sang dương => x = 2 là điểm cực tiểu.
Bước 4: Khoảng đồng biến, nghịch biến: y' > 0 khi x < 0 hoặc x > 2 => Hàm số đồng biến trên (-∞; 0) và (2; +∞). y' < 0 khi 0 < x < 2 => Hàm số nghịch biến trên (0; 2).
Bước 5: Tìm điểm uốn: 6x - 6 = 0 => x = 1. Tại x = 1, y'' đổi dấu => x = 1 là điểm uốn.
Khi giải bài toán này, học sinh cần chú ý:
Việc giải quyết bài toán về khảo sát hàm số bằng đạo hàm có nhiều ứng dụng thực tế, chẳng hạn như:
Giaitoan.edu.vn hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn khi giải quyết Câu 28 trang 76 SGK Đại số và Giải tích 11 Nâng cao và các bài toán tương tự.