Giải Câu 10 Trang 17 SGK Đại số và Giải tích 11 Nâng cao

Câu 10 trang 17 SGK Đại số và Giải tích 11 Nâng cao

Câu 10 trang 17 SGK Đại số và Giải tích 11 Nâng cao là một bài toán quan trọng trong chương trình học.

Bài toán này yêu cầu học sinh vận dụng kiến thức về hàm số, đồ thị hàm số và các phép biến đổi hình học để tìm ra lời giải chính xác.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.

Chứng minh rằng mọi giao điểm của đường thẳng xác định bởi phương trình với đồ thị của hàm số y = sinx đều cách gốc tọa độ một khoảng nhỏ hơn

Đề bài

Chứng minh rằng mọi giao điểm của đường thẳng xác định bởi phương trình \(y = {x \over 3}\) với đồ thị của hàm số \(y = \sin x\) đều cách gốc tọa độ một khoảng nhỏ hơn \(\sqrt {10} \)

Lời giải chi tiết

Đường thẳng \(y = {x \over 3}\) đi qua các điểm \(E(-3 ; -1)\) và \(F(3 ; 1)\)

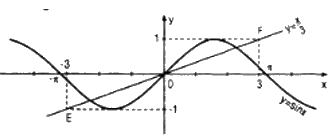
Câu 10 trang 17 SGK Đại số và Giải tích 11 Nâng cao 1

Chỉ có đoạn thẳng \(EF\) của đường thẳng đó nằm trong dải \(\left\{ {\left( {x{\rm{ }};{\rm{ }}y} \right)| - 1{\rm{ }} \le {\rm{ }}y{\rm{ }} \le {\rm{ }}1} \right\}\) (dải này chứa đồ thị của hàm số \(y = \sin x\)).

Vậy các giao điểm của đường thẳng \(y = {x \over 3}\) với đồ thị của hàm số \(y = \sin x\) phải thuộc đoạn \(EF\).

Mọi điểm của đoạn thẳng này cách \(O\) một khoảng không dài hơn \(OE=OF=\sqrt {3^2 + 1^2} = \sqrt {10} \)

Rõ ràng \(E, F\) không thuộc đồ thị của hàm số \(y = \sin x\) nên khoảng cách từ các giao điểm đến O nhỏ hơn \(\sqrt {10}\).

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Câu 10 trang 17 SGK Đại số và Giải tích 11 Nâng cao – hành trang không thể thiếu trong chuyên mục toán 11 trên nền tảng tài liệu toán. Bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Câu 10 Trang 17 SGK Đại số và Giải tích 11 Nâng cao: Phân tích Chi Tiết và Lời Giải

Bài toán Câu 10 trang 17 trong sách giáo khoa Đại số và Giải tích 11 Nâng cao thường xoay quanh việc xét tính đơn điệu của hàm số, tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số, hoặc giải phương trình, bất phương trình liên quan đến hàm số. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về:

Định nghĩa hàm số: Hiểu rõ khái niệm hàm số, tập xác định, tập giá trị.
Các loại hàm số: Hàm số bậc nhất, bậc hai, hàm số mũ, hàm số logarit, hàm số lượng giác và các tính chất của chúng.
Đạo hàm: Nắm vững các quy tắc tính đạo hàm, ý nghĩa hình học và vật lý của đạo hàm.
Ứng dụng của đạo hàm: Khảo sát hàm số, tìm cực trị, giải phương trình, bất phương trình.

Lời Giải Chi Tiết Câu 10 Trang 17

Để minh họa, giả sử Câu 10 trang 17 yêu cầu xét tính đơn điệu của hàm số f(x) = x³ - 3x² + 2. Chúng ta sẽ thực hiện các bước sau:

Tính đạo hàm: f'(x) = 3x² - 6x
Tìm điểm dừng: Giải phương trình f'(x) = 0, ta được x = 0 và x = 2.
Lập bảng biến thiên: Xét dấu f'(x) trên các khoảng (-∞, 0), (0, 2), (2, +∞).
Kết luận: Hàm số đồng biến trên các khoảng (-∞, 0) và (2, +∞), nghịch biến trên khoảng (0, 2).

Các Dạng Bài Tập Liên Quan

Ngoài việc xét tính đơn điệu, Câu 10 trang 17 và các bài tập tương tự có thể xuất hiện dưới các dạng khác nhau:

Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: Sử dụng đạo hàm để tìm cực trị và so sánh với giá trị tại các điểm biên.
Giải phương trình, bất phương trình: Vận dụng các kiến thức về đạo hàm, tính đơn điệu để giải quyết.
Khảo sát hàm số: Xác định tập xác định, tập giá trị, điểm đồng biến, nghịch biến, cực trị, điểm uốn, tiệm cận.

Mẹo Giải Bài Tập Đại Số và Giải tích 11 Nâng cao

Để học tốt môn Đại số và Giải tích 11 Nâng cao, bạn nên:

Nắm vững kiến thức cơ bản: Đọc kỹ sách giáo khoa, ghi chép bài giảng đầy đủ.
Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng.
Sử dụng các công cụ hỗ trợ: Máy tính bỏ túi, phần mềm vẽ đồ thị, các trang web học toán online.
Hỏi thầy cô, bạn bè: Khi gặp khó khăn, đừng ngần ngại hỏi để được giúp đỡ.

Ví dụ Minh Họa Thêm

Giả sử bài toán yêu cầu tìm giá trị nhỏ nhất của hàm số g(x) = x² - 4x + 5. Ta có thể giải như sau:

Tính đạo hàm: g'(x) = 2x - 4
Tìm điểm dừng: Giải phương trình g'(x) = 0, ta được x = 2.
Kiểm tra điều kiện cực trị: g''(x) = 2 > 0, vậy x = 2 là điểm cực tiểu.
Tính giá trị cực tiểu: g(2) = 2² - 4*2 + 5 = 1.
Kết luận: Giá trị nhỏ nhất của hàm số là 1.

Kết Luận

Câu 10 trang 17 SGK Đại số và Giải tích 11 Nâng cao là một bài tập điển hình để rèn luyện các kỹ năng giải toán liên quan đến hàm số. Bằng cách nắm vững kiến thức cơ bản, luyện tập thường xuyên và áp dụng các mẹo giải bài tập, bạn có thể tự tin giải quyết mọi bài toán tương tự.