Bài toán này thường yêu cầu học sinh vận dụng kiến thức về hàm số, đạo hàm, hoặc các khái niệm khác đã học để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hình 5.4 là đồ thị của hàm số y = f(x) trên
Đề bài
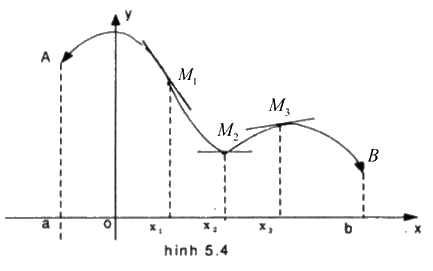
Hình 5.4 là đồ thị của hàm số y = f(x) trên khoảng (a ; b). Biết rằng tại các điểm M1, M2 và M3, đồ thị hàm số có tiếp tuyến được thể hiện trên hình vẽ. Dựa vào hình vẽ, em hãy nêu nhận xét về dấu của \(f'\left( {{x_1}} \right),f'\left( {{x_2}} \right)\,va\,f'\left( {{x_3}} \right)\)
Lời giải chi tiết
Đồ thị của hàm số y = f(x) có tiếp tuyến tại các điểm M1, M2 và M3 nên hàm số y = f(x) có đạo hàm tại các điểm x1, x2 và x3. Ta nhận thấy :
+ Tiếp tuyến tại các điểm M1 là một đường thẳng “đi xuống” từ trái sang phải, nên hệ số góc của tiếp tuyến là một số âm, suy ra \(f'\left( {{x_1}} \right) < 0\)
+ Tiếp tuyến tại điểm M2 là một đường thẳng song song với trục hoành nên hệ số góc của tiếp tuyến bằng 0, suy ra \(f'\left( {{x_2}} \right) = 0\)
+ Tiếp tuyến tại điểm M3 là một đường thẳng “đi lên” từ trái sang phải, nên hệ số góc của tiếp tuyến là một số dương, suy ra \(f'\left( {{x_3}} \right) > 0\)
Câu 12 trang 195 SGK Đại số và Giải tích 11 Nâng cao thường thuộc các dạng bài tập về ứng dụng đạo hàm để khảo sát hàm số, tìm cực trị, hoặc giải phương trình, bất phương trình. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, điều kiện cần và đủ để hàm số đạt cực trị, và các phương pháp giải phương trình, bất phương trình thường gặp.
Trước khi bắt đầu giải, hãy đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Xác định hàm số cần khảo sát, các điều kiện ràng buộc, và mục tiêu cần đạt được (ví dụ: tìm cực trị, tìm khoảng đơn điệu, giải phương trình). Việc phân tích đề bài kỹ lưỡng sẽ giúp bạn định hướng giải quyết bài toán một cách chính xác.
Giả sử đề bài yêu cầu khảo sát hàm số y = x3 - 3x2 + 2. Chúng ta sẽ áp dụng các bước giải trên để giải quyết bài toán này.
y' = 3x2 - 6x
3x2 - 6x = 0 => x = 0 hoặc x = 2
y'' = 6x - 6
y''(0) = -6 < 0 => Hàm số đạt cực đại tại x = 0
y''(2) = 6 > 0 => Hàm số đạt cực tiểu tại x = 2
Khi giải các bài tập về ứng dụng đạo hàm, cần chú ý đến các điểm sau:
Để củng cố kiến thức, bạn có thể thử giải các bài tập tương tự sau:
Câu 12 trang 195 SGK Đại số và Giải tích 11 Nâng cao là một bài toán điển hình về ứng dụng đạo hàm để khảo sát hàm số. Việc nắm vững các kiến thức cơ bản và áp dụng đúng các bước giải sẽ giúp bạn giải quyết bài toán một cách hiệu quả. Chúc bạn học tốt!