Bài toán này thường yêu cầu học sinh vận dụng kiến thức về vectơ, đường thẳng và mặt phẳng để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Cho tứ diện ABCD. Tìm điểm O cách đều bốn đỉnh của tứ diện.
Đề bài
Cho tứ diện ABCD. Tìm điểm O cách đều bốn đỉnh của tứ diện.
Lời giải chi tiết
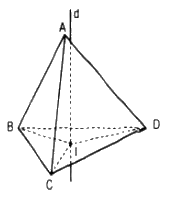
Gọi I là tâm đường tròn ngoại tiếp của ΔBCD
Gọi d là đường thẳng đi qua I và vuông góc với mặt phẳng (BCD)
Theo kết quả bài 14. M ϵ d ⇔ MB = MC = MD
(d gọi là trục của đường tròn ngoại tiếp tam giác BCD)
Gọi O là giao điểm của d với mặt phẳng trung trực của AB.
=> OA = OB ( vì O thuộc mặt phẳng trung trực của AB).
Và OB = OC = OD ( vì O thuộc đường thẳng d).
Suy ra :OA = OB = OC = OD hay O cách đều bốn đỉnh của tứ diện (O gọi là tâm mặt cầu ngoại tiếp tứ diện ABCD).
Câu 15 trang 102 SGK Hình học 11 Nâng cao thường thuộc chương trình học về vectơ trong không gian, đặc biệt là các bài toán liên quan đến quan hệ song song, vuông góc giữa đường thẳng và mặt phẳng. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản sau:
Trước khi bắt tay vào giải, hãy đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, lập kế hoạch giải bằng cách:
(Giả sử đề bài Câu 15 trang 102 SGK Hình học 11 Nâng cao là: Cho điểm A(1;2;3) và mặt phẳng (P): 2x - y + z - 5 = 0. Hãy tìm tọa độ điểm đối xứng của A qua mặt phẳng (P).)
Bước 1: Tìm hình chiếu vuông góc H của A lên mặt phẳng (P).
Đường thẳng Δ đi qua A và vuông góc với (P) có phương trình tham số:
x = 1 + 2t
y = 2 - t
z = 3 + t
Thay vào phương trình (P), ta được: 2(1 + 2t) - (2 - t) + (3 + t) - 5 = 0 => t = 0
Vậy H(1;2;3).
Bước 2: Tìm tọa độ điểm A' đối xứng với A qua mặt phẳng (P).
H là trung điểm của AA', suy ra:
xA' = 2xH - xA = 2(1) - 1 = 1
yA' = 2yH - yA = 2(2) - 2 = 2
zA' = 2zH - zA = 2(3) - 3 = 3
Vậy A'(1;2;3).
Kết luận: Điểm đối xứng của A qua mặt phẳng (P) là A'(1;2;3).
Ngoài dạng bài tập tìm điểm đối xứng, Câu 15 trang 102 SGK Hình học 11 Nâng cao và các bài tập tương tự có thể xuất hiện các dạng bài sau:
Để giải các dạng bài tập này, học sinh cần nắm vững các kiến thức cơ bản và luyện tập thường xuyên. Việc sử dụng các công cụ hỗ trợ như máy tính bỏ túi, phần mềm hình học có thể giúp tăng tốc độ và độ chính xác trong quá trình giải toán.
Để củng cố kiến thức và kỹ năng giải toán, bạn nên luyện tập thêm các bài tập tương tự trong SGK, sách bài tập và các đề thi thử. Ngoài ra, bạn có thể tham khảo các tài liệu học tập trực tuyến, các video hướng dẫn giải toán trên YouTube, v.v.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Chúc bạn học tập tốt!