Bài toán này thường yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ, và ứng dụng vào hình học không gian.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và kỹ năng giải bài tập.
Cho hai mặt phẳng vuông góc (P) và (Q) có giao tuyến Δ. Lấy A, B cùng thuộc Δ và lấy C ϵ (P), D ϵ (Q) sao cho AC ⊥ AB, BD ⊥ AB và AB = AC = BD. Xác định thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (α) đi qua điểm A và vuông góc với CD. Tính diện tích thiết diện khi AC = AB = BD = a.
Đề bài
Cho hai mặt phẳng vuông góc \((P)\) và \((Q)\) có giao tuyến \(Δ\). Lấy \(A, B\) cùng thuộc \(Δ\) và lấy \(C ϵ (P), D ϵ (Q)\) sao cho \(AC ⊥ AB, BD ⊥ AB\) và \(AB = AC = BD\). Xác định thiết diện của tứ diện \(ABCD\) khi cắt bởi mặt phẳng \((α)\) đi qua điểm \(A\) và vuông góc với \(CD\). Tính diện tích thiết diện khi \(AC = AB = BD = a.\)
Phương pháp giải - Xem chi tiết
+ Xác định mp \((α)\) và tìm thiết diện
+ Tình diện tích thiết diện.
Lời giải chi tiết
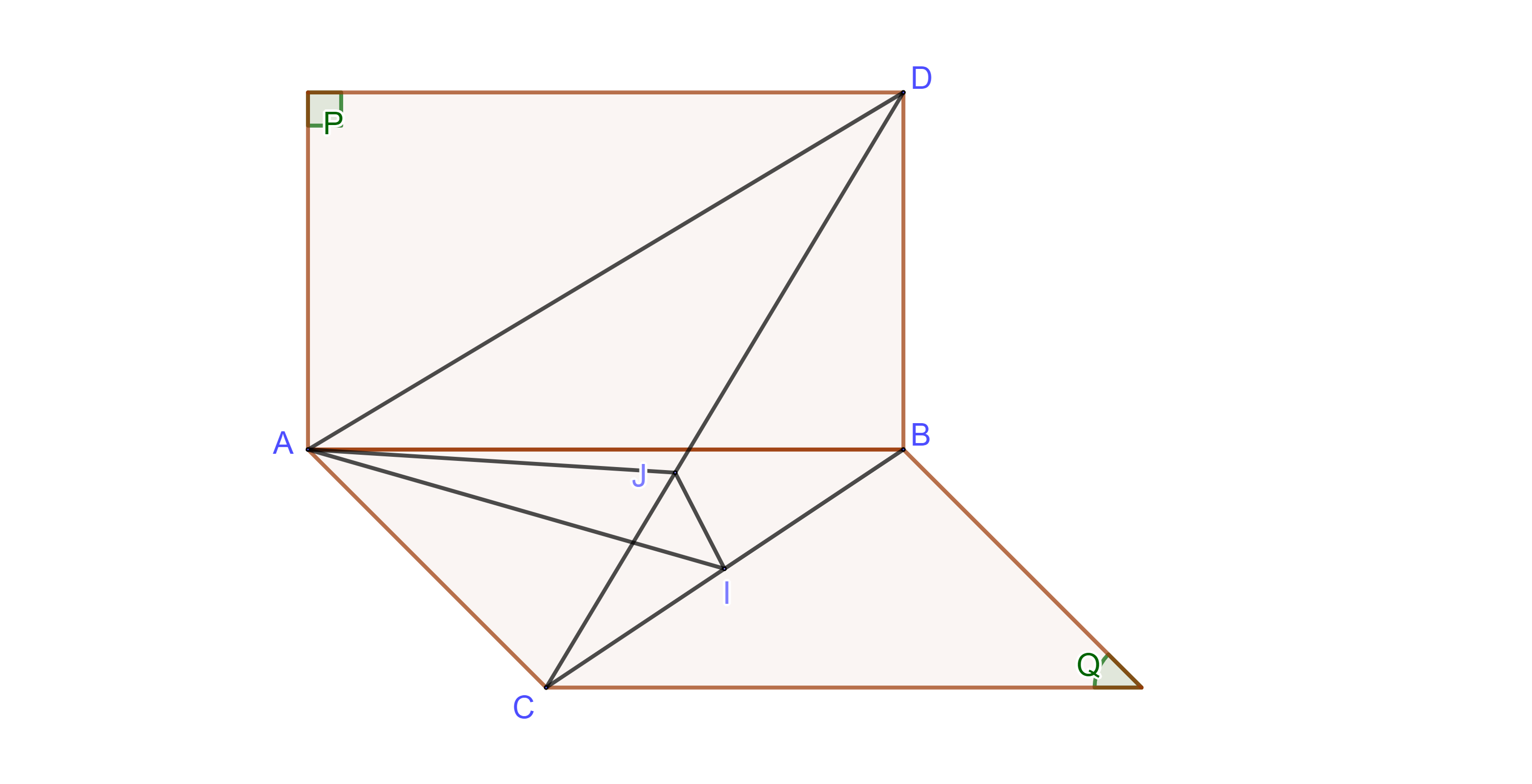
+) Xác định mặt phẳng \((α)\) và thiết diện.
Gọi \(I\) là trung điểm của \(BC\).
Ta có: \(AI ⊥ BC\) vì \(AC=AB\). (1)
Do \(BD ⊥ AB\) - là giao tuyến chung nên \(BD ⊥ mp(ABC) \Rightarrow BD ⊥ AI.\) (2)
Từ (1) và (2) \(\Rightarrow AI ⊥ (DBC) \subset DC .\)
Trong \(mp(DCB)\), từ \(I\), kẻ \(IJ ⊥ CD (J ϵ CD)\)
\(\Rightarrow DC ⊥ AI \) và \(DC ⊥ IJ\)
\(\Rightarrow DC ⊥ (AIJ) \)
Vậy \(mp(AIJ)\) chính là mặt phẳng \((α)\) và thiết diện phải tìm là tam giác \(AIJ\).
+) Tính diện tích tam giác \(AIJ\)
Ta có: tam giác \(AIJ\) vuông tại \(I\) vì \( AI ⊥ (DBC) \subset IJ .\)
Vậy \({S_{AIJ}} = \frac{1}{2}.AI.IJ\)
Tam giác \(ABC\) vuông tại \(A\) nên \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt 2 a\)
Và \( AI = CI = BI = \frac{{BC}}{2} = \frac{{\sqrt 2 a}}{2}\)
Lại có: \(\Delta CIJ\) đồng dạng với \(\Delta CDB\) (chung góc \(C\) và \(\hat J = \hat B = 90^0\))
\( \Rightarrow \frac{{IJ}}{{DB}} = \frac{{CI}}{{CD}} \Rightarrow IJ = DB.\frac{{CI}}{{CD}}\)
Mà \(DB = a,\;\;CI = \frac{{\sqrt 2 a}}{2};\;\;CD = \sqrt {B{C^2} + B{D^2}} = \sqrt 3 a\)
\( \Rightarrow IJ = a.\frac{{a\sqrt 2 }}{2}:\sqrt 3 a = \frac{{a\sqrt 6 }}{6}\)
\( \Rightarrow {S_{AIJ}} = \frac{1}{2}.\frac{{a\sqrt 2 }}{2}.\frac{{a\sqrt 6 }}{6} = \frac{{{a^2}\sqrt 3 }}{{12}}\)
Câu 25 trang 112 SGK Hình học 11 Nâng cao thường thuộc chương trình học về vectơ trong không gian. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Trước khi bắt đầu giải bài toán, điều quan trọng là phải đọc kỹ đề bài, phân tích các thông tin đã cho và xác định yêu cầu của bài toán. Thông thường, đề bài sẽ cung cấp các thông tin về các điểm, đường thẳng, mặt phẳng trong không gian, và yêu cầu tính toán một đại lượng nào đó, chẳng hạn như:
Dưới đây là một số phương pháp giải thường được sử dụng để giải quyết Câu 25 trang 112 SGK Hình học 11 Nâng cao:
Giả sử đề bài yêu cầu tính khoảng cách giữa hai điểm A(x1, y1, z1) và B(x2, y2, z2) trong không gian. Ta có thể sử dụng công thức sau:
AB = √((x2 - x1)² + (y2 - y1)² + (z2 - z1)²)
Khi giải Câu 25 trang 112 SGK Hình học 11 Nâng cao, học sinh cần lưu ý một số điểm sau:
Để củng cố kiến thức và kỹ năng giải bài tập về vectơ, học sinh có thể làm thêm một số bài tập tương tự, chẳng hạn như:
Câu 25 trang 112 SGK Hình học 11 Nâng cao là một bài toán quan trọng, giúp học sinh rèn luyện kỹ năng giải bài tập về vectơ trong không gian. Bằng cách nắm vững các khái niệm cơ bản, phương pháp giải chi tiết, và lưu ý các điểm quan trọng, học sinh có thể tự tin giải quyết bài toán này một cách hiệu quả.
| Khái niệm | Định nghĩa |
|---|---|
| Vectơ | Một đoạn thẳng có hướng, được xác định bởi điểm gốc và điểm cuối. |
| Tích vô hướng | Một phép toán giữa hai vectơ, cho ra một số thực. |
| Tích có hướng | Một phép toán giữa hai vectơ, cho ra một vectơ vuông góc với cả hai vectơ ban đầu. |