Chào mừng bạn đến với bài giải chi tiết Câu 4 trang 79 SGK Hình học 11 Nâng cao trên giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải đầy đủ, dễ hiểu, giúp bạn nắm vững kiến thức và kỹ năng giải toán hình học.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, hỗ trợ bạn trong quá trình chinh phục môn Toán.
Cho hình chóp S.ABCD. Gọi AC ∩ BD = I, AB ∩ CD = J, AD ∩ BC = K. Đẳng thức nào sai trong các đẳng thức sau đây ?
Đề bài
Cho hình chóp S.ABCD. Gọi AC ∩ BD = I, AB ∩ CD = J, AD ∩ BC = K. Đẳng thức nào sai trong các đẳng thức sau đây ?
A. (SAC) ∩ (SBD) = SI
B. (SAB) ∩ (SCD) = SJ
C. (SAD) ∩ (SBC) = SK
D. (SAC) ∩ (SAD) = AB
Lời giải chi tiết
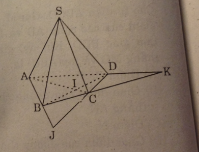
(SAC) ∩ (SAD) = SA
Chọn (D)
Câu 4 trang 79 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học, thường tập trung vào việc vận dụng các kiến thức về vectơ, quan hệ song song, quan hệ vuông góc trong không gian. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các định nghĩa, tính chất và định lý liên quan.
(Nội dung đề bài sẽ được chèn vào đây. Ví dụ:) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).
Để tìm góc giữa đường thẳng SC và mặt phẳng (ABCD), ta cần xác định hình chiếu của điểm S lên mặt phẳng (ABCD). Trong trường hợp này, hình chiếu của S là điểm A. Do đó, góc cần tìm chính là góc SCA.
Vì ABCD là hình vuông cạnh a, nên AC = a√2 (theo định lý Pitago).
Tam giác SAC vuông tại A, nên SC = √(SA² + AC²) = √(a² + (a√2)²) = √(a² + 2a²) = a√3.
Trong tam giác SAC vuông tại A, ta có: tan(∠SCA) = SA/AC = a/(a√2) = 1/√2. Do đó, ∠SCA = arctan(1/√2) ≈ 35.26°.
Vậy, góc giữa đường thẳng SC và mặt phẳng (ABCD) là arctan(1/√2) ≈ 35.26°.
Để hiểu sâu hơn về bài toán này, bạn có thể thử giải các bài tập tương tự với các thông số khác nhau. Ví dụ:
Để giải quyết bài toán này, bạn cần nắm vững các kiến thức sau:
Học Toán Hình học 11 Nâng cao đòi hỏi sự kiên trì và luyện tập thường xuyên. Dưới đây là một số lời khuyên:
Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!