Bài tập Câu 8 trang 35 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học Hình học 11. Bài toán này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, cùng với phương pháp giải bài toán một cách khoa học và hiệu quả.
Cho đường tròn (O) có đường kính AB.
Đề bài
Cho đường tròn (O) có đường kính AB. Gọi C là điểm đối xứng với A và B và PQ là đường kính thay đổi của (O) khác đường kính AB. Đường thẳng CQ cắt PA và PB lần lượt tại M và N
a. Chứng minh rằng Q là trung điểm của CM, N là trung điểm của CQ.
b. Tìm quỹ tích các điểm M và N khi đường kính PQ thay đổi
Lời giải chi tiết
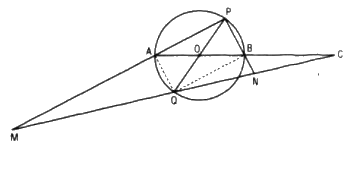
a. Ta có QB // AP (vì cùng vuông góc với PB) và B là trung điểm của AC nên Q là trung điểm của CM
Ta có AQ // BN (vì cùng vuông góc với AP) và B là trung điểm của AC nên N là trung điểm của CQ
b. Theo câu a) ta có \(\overrightarrow {CM} = 2\overrightarrow {CQ} \) nên phép vị tự V tâm C tỉ số 2 biến Q thành M
Vì Q chạy trên đường tròn (O) (trừ hai điểm A, B) nên quỹ tích M là ảnh của đường tròn đó qua phép vị tự V tâm C tỉ số 2 (trừ ảnh của A, B)
Tương tự, ta có \(\overrightarrow {CN} = {1 \over 2}\overrightarrow {CQ} \) nên quỹ tích N là ảnh của đường tròn (O) qua phép vị tự V tâm C, tỉ số \({1 \over 2}\) (trừ ảnh của A, B)
Câu 8 trang 35 SGK Hình học 11 Nâng cao thuộc chương trình Hình học không gian, cụ thể là phần vectơ trong không gian. Bài toán này thường yêu cầu học sinh chứng minh một đẳng thức vectơ, xác định mối quan hệ giữa các vectơ, hoặc giải quyết một bài toán liên quan đến hình học không gian bằng phương pháp vectơ.
Để hiểu rõ hơn về bài toán, chúng ta cần xem xét lại lý thuyết cơ bản về vectơ. Vectơ là một đoạn thẳng có hướng, được xác định bởi điểm gốc và điểm cuối. Các phép toán vectơ bao gồm:
Để giải quyết bài toán Câu 8 trang 35 SGK Hình học 11 Nâng cao, học sinh cần:
Đề bài: Cho hình hộp ABCD.A'B'C'D'. Gọi M là trung điểm của cạnh AB. Chứng minh rằng: overrightarrow{AM} = 1/2overrightarrow{AC'}.
Lời giải:
Ta có: overrightarrow{AM} = 1/2overrightarrow{AB}.
Mặt khác, overrightarrow{AC'} = overrightarrow{AB} + overrightarrow{BC'} = overrightarrow{AB} + overrightarrow{AD}.
Do đó, 1/2overrightarrow{AC'} = 1/2(overrightarrow{AB} + overrightarrow{AD}).
Để chứng minh overrightarrow{AM} = 1/2overrightarrow{AC'}, ta cần chứng minh overrightarrow{AB} = overrightarrow{AB} + overrightarrow{AD}, điều này không đúng.
(Lưu ý: Đây chỉ là một ví dụ minh họa, lời giải cụ thể sẽ phụ thuộc vào nội dung chính xác của Câu 8 trang 35 SGK Hình học 11 Nâng cao.)
Để học tốt và giải quyết hiệu quả các bài tập về vectơ trong không gian, học sinh nên:
Hy vọng với những phân tích và hướng dẫn trên, các bạn học sinh sẽ tự tin hơn khi giải quyết Câu 8 trang 35 SGK Hình học 11 Nâng cao và các bài tập tương tự.