Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Xác định tâm vị tự trong và tâm vị tự ngoài của hai đường tròn trong các trường hợp sau :
Hai đường tròn tiếp xúc ngoài với nhau
Phương pháp giải:
Cách xác định tâm vị tự:
- Lấy điểm \(M\) thuộc đường tròn \((O)\).
- Qua \(O'\) kẻ đường thẳng song song với \(OM\), đường thẳng này cắt đường tròn \((O')\) tại \(M'\) và \(M''\).
- Hai đường thẳng \(MM'\) và \(MM''\) cắt đường thẳng \(OO'\) theo thứ tự \(I\) và \(I'\).
Khi đó, \(I\) và \(I'\) là các tâm vị tự cần tìm.
Lời giải chi tiết:
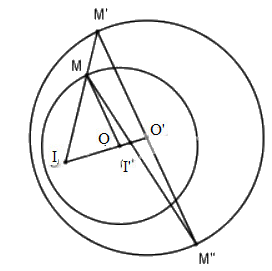
Gọi I là tâm vị tự ngoài, I’ là tâm vị tự trong của hai đường tròn \((O)\) và \((O’)\)
Nếu \((O)\) và \((O’)\) tiếp xúc ngoài thì tiếp điểm I’ là tâm vị tự trong, giao điểm của OO’ với tiếp tuyến chung ngoài của \((O)\) và \((O’)\) (nếu có) là tâm vị tự ngoài (h.a)
Hai đường tròn tiếp xúc trong với nhau
Lời giải chi tiết:

Nếu \((O)\) và \((O’)\) tiếp xúc trong thì tiếp điểm I là tâm vị tự ngoài, tâm vị tự trong I’ xác định như hình vẽ b)
Một đường tròn chứa đường tròn kia
Lời giải chi tiết:

Nếu \((O')\) chứa \((O)\) thì xác định I và I’ như hình vẽ (đặc biệt, khi O trùng O’ thì I và I’ trùng O)
Bài tập 27 trang 29 SGK Hình học 11 Nâng cao thuộc chương trình học Hình học lớp 11, tập trung vào việc củng cố kiến thức về vectơ và ứng dụng của chúng trong giải quyết các bài toán hình học. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và đặc biệt là các tính chất của vectơ trong các hình bình hành, tam giác.
(Nội dung đề bài sẽ được chèn vào đây - ví dụ: Cho hình bình hành ABCD. Gọi M là trung điểm của BC. N là giao điểm của AM và BD. Chứng minh rằng BN = 2ND.)
Để giải bài toán này, chúng ta sẽ sử dụng phương pháp tọa độ vectơ. Phương pháp này cho phép chúng ta biểu diễn các điểm và vectơ bằng tọa độ, từ đó sử dụng các phép toán đại số để chứng minh các mối quan hệ hình học. Các bước thực hiện như sau:
(Lời giải chi tiết sẽ được trình bày ở đây, bao gồm các bước chọn hệ tọa độ, biểu diễn tọa độ các điểm và vectơ, thực hiện các phép toán vectơ, và chứng minh kết quả. Lời giải cần được trình bày rõ ràng, dễ hiểu, và có đầy đủ các bước giải thích.)
Để giúp bạn hiểu rõ hơn về phương pháp giải bài toán vectơ, chúng ta sẽ xem xét một ví dụ minh họa:
(Ví dụ minh họa sẽ được trình bày ở đây, bao gồm đề bài, lời giải, và các giải thích chi tiết.)
Ngoài phương pháp tọa độ vectơ, còn có một số phương pháp khác để giải bài toán vectơ, chẳng hạn như phương pháp hình học thuần túy. Tuy nhiên, phương pháp tọa độ vectơ thường được sử dụng phổ biến hơn vì tính đơn giản và hiệu quả của nó.
Để củng cố kiến thức về vectơ và ứng dụng của chúng trong giải quyết các bài toán hình học, bạn có thể tham khảo các bài tập tương tự sau:
Câu 27 trang 29 SGK Hình học 11 Nâng cao là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và ứng dụng của chúng trong giải quyết các bài toán hình học. Bằng cách nắm vững phương pháp giải bài toán vectơ và luyện tập thường xuyên, bạn có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Hình học.