Giải Câu 32 Trang 68 SGK Hình Học 11 Nâng Cao

Câu 32 trang 68 SGK Hình học 11 Nâng cao

Giải Câu 32 Trang 68 SGK Hình Học 11 Nâng Cao

Bài tập Câu 32 trang 68 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học Hình học không gian lớp 11. Bài toán này thường yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng vào giải quyết các bài toán liên quan đến hình học không gian.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu và các phương pháp giải khác nhau để giúp bạn nắm vững kiến thức và tự tin giải quyết các bài toán tương tự.

Cho hai đường thẳng chéo nhau a và b lần lượt nằm trên hai mặt phẳng song song (P) và (Q). Chứng minh rằng nếu điểm M không nằm trên (P) và không nằm trên (Q) thì có duy nhất một đường thẳng đi qua M cắt cả a và b

Đề bài

Lời giải chi tiết

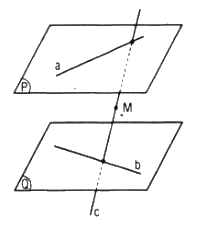
Câu 32 trang 68 SGK Hình học 11 Nâng cao 2

Giả sử c = mp ( M, a) ∩ mp(M, b). Ta cần chứng minh c cắt cả a và b.

Vì c và a cũng nằm trên một mặt phẳng và không thể trùng nhau ( do c qua M và a không đi qua M) nên hoặc c // a hoặc c cắt a. Cũng vậy, hoặc c // b hoặc c cắt b.

Không thể xảy ra đồng thời c // a; c // b vì a và b chéo nhau. Vậy nếu c song song với a và c phải cắt b, tức là c qua một điểm của mp (Q) và song song với a, suy ra c phải thuộc mp (Q), và do đó M thuộc (Q) (trái giả thiết).

Tương tự, không thể có c song song với b.

Tóm lại c cắt a và b.

Nếu còn có đường thẳng c’ khác c đi qua M, cắt cả a và b thì a và b đồng phẳng. Vô lí.

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Câu 32 trang 68 SGK Hình học 11 Nâng cao – hành trang không thể thiếu trong chuyên mục Học tốt Toán lớp 11 trên nền tảng học toán. Bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải Chi Tiết Câu 32 Trang 68 SGK Hình Học 11 Nâng Cao

Bài tập 32 trang 68 SGK Hình học 11 Nâng cao thuộc chương trình học về vectơ trong không gian. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:

Vectơ: Định nghĩa, các phép toán cộng, trừ, nhân với một số thực.
Tích vô hướng của hai vectơ: Công thức tính, ứng dụng để tính góc giữa hai vectơ, kiểm tra tính vuông góc.
Hệ tọa độ trong không gian: Biểu diễn vectơ bằng tọa độ, các phép toán vectơ trong hệ tọa độ.

Phân Tích Đề Bài và Lập Kế Hoạch Giải

Trước khi bắt tay vào giải bài tập, điều quan trọng là phải đọc kỹ đề bài, xác định rõ yêu cầu và các dữ kiện đã cho. Sau đó, lập kế hoạch giải bài tập bằng cách xác định các bước cần thực hiện và các công thức, định lý cần sử dụng.

Lời Giải Chi Tiết

(Giả sử đề bài là: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).)

Bước 1: Chọn hệ tọa độ thích hợp. Đặt gốc tọa độ tại A, các trục Ox, Oy, Oz lần lượt trùng với các đường thẳng AB, AD, SA.
Bước 2: Xác định tọa độ các điểm.
- A(0; 0; 0)
- B(a; 0; 0)
- C(a; a; 0)
- D(0; a; 0)
- S(0; 0; a)
Bước 3: Tìm vectơ chỉ phương của đường thẳng SC. SC = (a; a; -a)
Bước 4: Tìm vectơ pháp tuyến của mặt phẳng (ABCD). n = (0; 0; 1)
Bước 5: Tính góc giữa đường thẳng SC và mặt phẳng (ABCD). Góc α giữa SC và (ABCD) được tính bởi công thức: sin(α) = |SC.n| / (||SC|| * ||n||).
Bước 6: Tính toán và kết luận. Tính toán các giá trị và suy ra góc α.

Các Dạng Bài Tập Tương Tự

Ngoài bài tập 32 trang 68, SGK Hình học 11 Nâng cao còn có nhiều bài tập tương tự liên quan đến vectơ trong không gian. Các bài tập này thường yêu cầu học sinh:

Tính tích vô hướng của hai vectơ.
Tính góc giữa hai vectơ.
Kiểm tra tính vuông góc của hai vectơ.
Tìm vectơ pháp tuyến của một mặt phẳng.
Tính khoảng cách từ một điểm đến một mặt phẳng.

Mẹo Giải Bài Tập Vectơ Trong Không Gian

Để giải tốt các bài tập về vectơ trong không gian, bạn có thể tham khảo một số mẹo sau:

Nắm vững các định nghĩa và công thức cơ bản.
Sử dụng hệ tọa độ để biểu diễn các vectơ và mặt phẳng.
Vận dụng các phép toán vectơ để đơn giản hóa bài toán.
Kiểm tra lại kết quả sau khi giải xong.

Ứng Dụng Của Vectơ Trong Hình Học Không Gian

Vectơ là một công cụ mạnh mẽ để giải quyết các bài toán trong hình học không gian. Chúng được sử dụng để:

Biểu diễn các điểm, đường thẳng, mặt phẳng.
Tính góc giữa hai đường thẳng, giữa đường thẳng và mặt phẳng.
Kiểm tra tính song song, vuông góc của các đường thẳng, mặt phẳng.
Giải các bài toán về khoảng cách.

Tổng Kết

Bài tập Câu 32 trang 68 SGK Hình học 11 Nâng cao là một bài tập điển hình để rèn luyện kỹ năng giải toán về vectơ trong không gian. Hy vọng với lời giải chi tiết và các hướng dẫn trên, bạn đã hiểu rõ cách giải bài tập này và có thể tự tin giải quyết các bài tập tương tự.