Bài toán này thường yêu cầu học sinh vận dụng kiến thức về vectơ, đường thẳng và mặt phẳng để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Cho hình tứ diện ABCD có AB = AC = AD và
AB ⊥ CD;
Lời giải chi tiết:
Ta có:
\(\eqalign{ & \overrightarrow {AB} .\overrightarrow {CD} \cr &= \overrightarrow {AB} .\left( {\overrightarrow {AD} - \overrightarrow {AC} } \right) \cr &= \overrightarrow {AB} .\overrightarrow {AD} - \overrightarrow {AB} .\overrightarrow {AC} \cr & = AB.AD.\cos \widehat {BAD} - AB.AC.\cos \widehat {BAC} = 0 \cr & \Rightarrow AB \bot CD. \cr} \)
(Vì AD=AC và \(\widehat {BAD}=\widehat {BAC}=60^0\).
Nếu I và J lần lượt là trung điểm của AB và CD thì \(IJ \bot AB\) và \(IJ \bot CD.\)
Lời giải chi tiết:
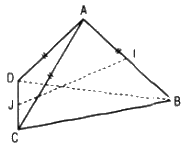
Ta có:
\(\eqalign{ & \overrightarrow {IJ} = \overrightarrow {IA} + \overrightarrow {AJ} \cr & = {1 \over 2}\overrightarrow {BA} + {1 \over 2}\left( {\overrightarrow {AD} + \overrightarrow {AC} } \right) \cr & = {1 \over 2}\left( {\overrightarrow {AD} + \overrightarrow {BC} } \right) \cr & = {1 \over 2}\left( {\overrightarrow {AD} + \overrightarrow {AC} - \overrightarrow {AB} } \right) \cr} \)
Suy ra :
\(\eqalign{ & \overrightarrow {AB} .\overrightarrow {IJ} = {1 \over 2}\left( {\overrightarrow {AB} .\overrightarrow {AD} + \overrightarrow {AB} .\overrightarrow {AC} - A{B^2}} \right) \cr & ={1 \over 2} \left( {AB.AD.\cos 60^\circ } + AB.AC.\cos 60^\circ - A{B^2} \right) \cr&= 0 \cr & \Rightarrow AB \bot IJ \cr} \)
Mặt khác :
\(\eqalign{ & \overrightarrow {CD} .\overrightarrow {IJ} = {1 \over 2}\left( {\overrightarrow {CA} + \overrightarrow {AD} } \right).\left( {\overrightarrow {AD} + \overrightarrow {BA} + \overrightarrow {AC} } \right) \cr & = {1 \over 2}\left( { - \overrightarrow {AC} .\overrightarrow {AD} + {{\overrightarrow {AD} }^2} + \overrightarrow {CA} .\overrightarrow {BA} + \overrightarrow {AD} .\overrightarrow {BA} - {{\overrightarrow {AC} }^2} + \overrightarrow {AD} .\overrightarrow {AC} } \right) \cr & = - {1 \over 2}\overrightarrow {AB} .\left( {\overrightarrow {CA} + \overrightarrow {AD} } \right) = - {1 \over 2}\overrightarrow {AB} .\overrightarrow {CD} = 0 \cr & \Rightarrow CD \bot IJ \cr} \)
Bài toán Câu 11 trang 96 SGK Hình học 11 Nâng cao thường xoay quanh các kiến thức về vectơ trong không gian, mối quan hệ giữa đường thẳng và mặt phẳng, và các ứng dụng của chúng trong việc chứng minh tính đồng phẳng, tính song song, và tính vuông góc. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các định nghĩa, tính chất, và định lý liên quan.
Trước khi đi vào giải chi tiết, chúng ta cần ôn lại một số kiến thức nền tảng:
Thông thường, bài toán Câu 11 trang 96 sẽ đưa ra một hình chóp hoặc một tứ diện, và yêu cầu chứng minh một mối quan hệ nào đó giữa các cạnh, các mặt, hoặc các vectơ liên quan. Ví dụ, bài toán có thể yêu cầu chứng minh:
Để giải quyết bài toán, chúng ta thường sử dụng các phương pháp sau:
Giả sử bài toán yêu cầu chứng minh hai đường thẳng song song. Chúng ta có thể thực hiện như sau:
Hoặc, nếu bài toán yêu cầu chứng minh một đường thẳng vuông góc với một mặt phẳng, chúng ta có thể thực hiện như sau:
Ngoài bài toán Câu 11 trang 96, học sinh cũng nên luyện tập các dạng bài tập tương tự để củng cố kiến thức và kỹ năng:
Để giải bài tập Hình học không gian hiệu quả, bạn nên:
Hy vọng với những phân tích và lời giải chi tiết trên, bạn sẽ tự tin hơn khi giải quyết bài toán Câu 11 trang 96 SGK Hình học 11 Nâng cao và các bài tập tương tự. Chúc bạn học tốt!