Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình hộp ABCD.A’B’C’D’. Trên ba cạnh AB, DD’, C’B’ lần lượt lấy ba điểm M, N, P không trùng với các đỉnh sao cho
Đề bài
Cho hình hộp ABCD.A’B’C’D’. Trên ba cạnh AB, DD’, C’B’ lần lượt lấy ba điểm M, N, P không trùng với các đỉnh sao cho \({{AM} \over {AB}} = {{D'N} \over {D'D}} = {{B'P} \over {B'C'}}\)
a. Chứng minh rằng mp(MNP) và mp(AB'D’) song song với nhau
b. Xác định thiết diện của hình hộp khi cắt bởi mp(MNP)
Lời giải chi tiết
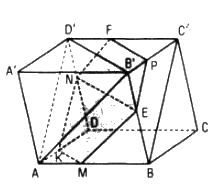
a. Kẻ ME song song với AB’ (E ∈ BB’) (1)
Ta có: \(\eqalign{ & {{B'E} \over {B'B}} = {{AM} \over {AB}} \Rightarrow {{B'E} \over {B'B}} = {{B'P} \over {B'C'}} \cr & \cr} \)
⇒ EP // BC’ ⇒EP // AD’ (2)
Từ (1) và (2) suy ra (MEP) // (AB’D’) (3)
Rõ ràng D’N = B’E nên EN // B’D’
Mà B’D’ ⊂ (AB’D’) và E ∈ (MEP) nên từ (3) suy ra EN ⊂ (MEP), tức (MNP) chính là (MEP)
Vậy (MNP) // (AB’D’)
b. Từ M kẻ ME song song với AB’, từ P kẻ PF song song với B’D’. Từ N kẻ NK song song với AD’ cắt AD tại K
Thiết diện là lục giác MEPFNK có các cạnh đối song song
Bài tập 7 trang 78 SGK Hình học 11 Nâng cao thường xoay quanh việc áp dụng các kiến thức về vectơ để chứng minh các tính chất hình học hoặc giải quyết các bài toán liên quan đến vị trí tương đối của các điểm và đường thẳng. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Để cung cấp một lời giải cụ thể, chúng ta cần biết nội dung chính xác của câu 7 trang 78. Tuy nhiên, dựa trên kinh nghiệm giảng dạy và phân tích các đề thi, chúng ta có thể đưa ra một ví dụ về dạng bài tập thường gặp và cách giải:
Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng: overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2
Lời giải:
Vì M là trung điểm của BC, ta có: overrightarrow{BM} =overrightarrow{MC}.
Áp dụng quy tắc cộng vectơ, ta có: overrightarrow{AM} =overrightarrow{AB} +overrightarrow{BM}.
Thay overrightarrow{BM} =overrightarrow{MC}, ta được: overrightarrow{AM} =overrightarrow{AB} +overrightarrow{MC}.
Lại có: overrightarrow{AC} =overrightarrow{AM} +overrightarrow{MC}, suy ra overrightarrow{MC} =overrightarrow{AC} -overrightarrow{AM}.
Thay vào phương trình trên, ta được: overrightarrow{AM} =overrightarrow{AB} +overrightarrow{AC} -overrightarrow{AM}.
Chuyển vế, ta có: 2overrightarrow{AM} =overrightarrow{AB} +overrightarrow{AC}.
Vậy: overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2 (đpcm).
Ngoài dạng bài tập chứng minh như trên, Câu 7 trang 78 SGK Hình học 11 Nâng cao có thể xuất hiện ở các dạng khác như:
Để giải các bài tập về vectơ một cách hiệu quả, bạn nên:
Câu 7 trang 78 SGK Hình học 11 Nâng cao là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và ứng dụng của vectơ trong hình học. Bằng cách nắm vững các khái niệm cơ bản, áp dụng các quy tắc và công thức, và luyện tập thường xuyên, bạn có thể tự tin giải quyết bài tập này và các bài tập tương tự.