Bài tập Câu 9 trang 13 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học Hình học không gian lớp 11. Bài toán này yêu cầu học sinh vận dụng kiến thức về vectơ, phép toán vectơ và các tính chất liên quan để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, cùng với phương pháp giải khoa học, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho góc nhọn
Đề bài
Cho góc nhọn xOy và một điểm A nằm trong góc đó. Hãy xác định điểm B trên Ox và điểm C trên Oy sao cho tam giác ABC có chu vi nhỏ nhất
Lời giải chi tiết
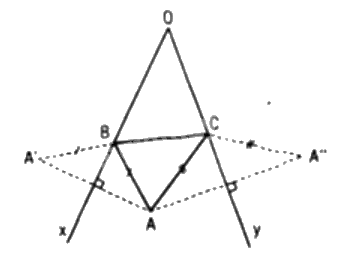
Xét tam giác bất kì ABC có B và C lần lượt nằm trên hai tia Ox và Oy.
Gọi A’ và A” là các điểm đối xứng với điểm A lần lượt qua các đường thẳng Ox và Oy.
Ta có \(AB = A’B\) và \(AC = A”C\) ( do các \(△ABA’\) và \(△ACA”\) là các tam giác cân).
Gọi \(2p\) là chu vi của tam giác ABC thì:
\(2p = AB + BC + CA \)\(= A’B + BC + CA” ≥ A’A”\)
Dấu “=” xảy ra khi bốn điểm \(A’, B, C, A”\) thẳng hàng.
Suy ra để chu vi tam giác ABC bé nhất thì phải lấy B và C lần lượt là giao điểm của đoạn thẳng A’A” với hai tia Ox và Oy (các giao điểm đó tồn tại vì góc xOy nhọn)
Câu 9 trang 13 SGK Hình học 11 Nâng cao thường xoay quanh việc áp dụng các kiến thức về vectơ trong không gian, đặc biệt là các phép toán vectơ như cộng, trừ, nhân với một số thực và tích vô hướng. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững định nghĩa, tính chất và các công thức liên quan đến vectơ.
Trước khi đi vào giải chi tiết, chúng ta cần ôn lại một số kiến thức cơ bản:
Đề bài thường yêu cầu:
(Giả sử đề bài là: Cho hai điểm A(1; 2; 3) và B(3; 4; 5). Tính độ dài đoạn thẳng AB và tìm tọa độ trung điểm I của đoạn thẳng AB.)
Lời giải:
Vectơ AB = (3-1; 4-2; 5-3) = (2; 2; 2)
Độ dài AB = |AB| = √(22 + 22 + 22) = √12 = 2√3
Tọa độ trung điểm I = ((1+3)/2; (2+4)/2; (3+5)/2) = (2; 3; 4)
Ngoài dạng bài tập tính độ dài và tìm trung điểm, Câu 9 trang 13 SGK Hình học 11 Nâng cao còn có thể xuất hiện các dạng bài tập sau:
Phương pháp giải:
Để nắm vững kiến thức và kỹ năng giải các bài tập về vectơ trong không gian, bạn nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Ngoài ra, bạn có thể tham gia các khóa học online hoặc tìm kiếm sự giúp đỡ từ các giáo viên, bạn bè.
Câu 9 trang 13 SGK Hình học 11 Nâng cao là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ trong không gian. Bằng cách nắm vững lý thuyết, phân tích đề bài một cách cẩn thận và áp dụng các phương pháp giải phù hợp, bạn có thể tự tin giải quyết bài toán này và các bài tập tương tự.