Chào mừng bạn đến với bài giải chi tiết Câu 37 trang 68 SGK Hình học 11 Nâng cao trên giaitoan.edu.vn. Bài tập này thuộc chương trình Hình học không gian, tập trung vào việc vận dụng kiến thức về vectơ và các phép toán vectơ trong không gian.
Chúng tôi cung cấp lời giải dễ hiểu, từng bước, giúp bạn nắm vững phương pháp giải và tự tin làm bài tập. Ngoài ra, bạn có thể tham khảo thêm các bài tập tương tự để củng cố kiến thức.
Cho hình hộp ABCD.A’B’C’D’. Chứng minh rẳng a. mp(BDA’) // mp(B’D’C) b.Đường chéo AC’ đi qua các trọng tâm G1, G2 của hai tam giác BDA’ và B’D’C
mp(BDA’) // mp(B’D’C)
Phương pháp giải:
Mặt phẳng (P) chứa hai đường thẳng cắt nhau cùng song song với (Q) thì (P)//(Q).
Lời giải chi tiết:
Chứng minh ( BDA’) // (B’D’C)
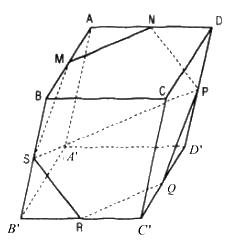
Tứ giác BB’D’D và A’B’CD là các hình bình hành nên : BD // B’D’ và DA’ // B’C
\(BD//B'D' \subset \left( {B'D'C} \right)\)\( \Rightarrow BD//\left( {B'D'C} \right)\)
\(DA'//CB' \subset \left( {B'D'C} \right)\)\( \Rightarrow DA'//\left( {B'D'C} \right)\)
Mà \(BD,DA' \subset \left( {A'BD} \right) \)\(\Rightarrow \left( {A'BD} \right)//\left( {B'D'C} \right)\)
Vậy (BDA’) // (B’D’C).
Đường chéo AC’ đi qua các trọng tâm G1, G2 của hai tam giác BDA’ và B’D’C
Lời giải chi tiết:

Chứng minh G1 , G2 ∈ AC’
Gọi O, O’ lần lượt là tâm của hình bình hành ABCD và A’B’C’D’.
Trong mặt phẳng (AA’C’C) gọi G1 , G2 lần lượt là giao điểm của AC’ với A’O và O’C.
Ta chứng minh G1, G2 lần lượt là trọng tâm của ∆A’BD và ∆CB’D’.
Thật vậy, ta có ∆G1OA đồng dạng ∆G1A’C’ ( vì AC // A’C’)
\( \Rightarrow {{{G_1}O} \over {{G_1}A'}} = {{OA} \over {A'C'}} = {1 \over 2} \Rightarrow {{A'{G_1}} \over {A'O}} = {2 \over 3}\)
⇒ G1 là trọng tâm ∆A’BD.
Tương tự, G2 là trọng tâm ∆CB’D’. Vậy AC’ đi qua G1, G2 .
G1 và G2 chia đoạn AC’ thành ba phần bằng nhau
Lời giải chi tiết:
Chứng minh AG1 = G1G2 = G2C’
Theo câu trên , ta có:
\({{A{G_1}} \over {{G_1}C'}} = {{AO} \over {A'C'}} = {1 \over 2}\) ( vì ∆G1OA đồng dạng ∆G1A’C’) \( \Rightarrow A{G_1} = {1 \over 3}AC'\) (1)
Tương tự: \({{C'{G_2}} \over {{G_2}A}} = {{C'O'} \over {CA}} = {1 \over 2}\) ( vì ∆G2C’O' đồng dạng ∆G2AC) \( \Rightarrow C'{G_2} = {1 \over 3}AC'\) (2)
Từ (1) và (2) suy ra: AG1 = G1G2 = G2C’.
Các trung điểm của sáu cạnh BC, CD, DD’, D’A’, A’B’,B’B cùng nằm trên một mặt phẳng
Lời giải chi tiết:

Gọi M, N, P, Q, S, R lần lượt là trung điểm của các cạnh AB, AD, DD’, C’D’, C’B’, B’B.
Ta có: \(\left\{ {\matrix{ {MN//BD} \cr {SP//BD} \cr } } \right. \Rightarrow MN//SP\)
Gọi (α) = (MN, SP)
Ta có : \(\left\{ {\matrix{ {PQ//DC'} \cr {MS//AB'} \cr } } \right. \Rightarrow PQ//MS\)
( vì DC’ // AB’)
⇒ PQ ⊂ (α) do đó Q ∈ (α).
Tương tự: QR // MN ⇒ QR ⊂ (α) do đó R ∈ (α).
Vậy M, N, P, Q, R, S ∈ (α).
Mặt khác vì \(\left\{ {\matrix{ {MS//AB'} \cr {NP//AD'} \cr } } \right.\) nên (MNPQRS) // (AB’D').
Bài tập 37 trang 68 SGK Hình học 11 Nâng cao là một bài toán điển hình về ứng dụng của vectơ trong không gian. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Trước khi bắt tay vào giải bài tập, chúng ta cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, lập kế hoạch giải cụ thể, bao gồm các bước thực hiện và các công thức cần sử dụng.
(Giả sử đề bài là: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).)
Ngoài bài tập 37 trang 68, SGK Hình học 11 Nâng cao còn có nhiều bài tập tương tự về ứng dụng của vectơ trong không gian. Các bài tập này thường yêu cầu học sinh:
Để giải tốt các bài tập về vectơ trong không gian, bạn có thể tham khảo một số mẹo sau:
Bài tập 37 trang 68 SGK Hình học 11 Nâng cao là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ trong không gian. Hy vọng với lời giải chi tiết và các phân tích trên, bạn đã hiểu rõ cách giải bài tập này và có thể tự tin giải các bài tập tương tự. Chúc bạn học tốt!
| Công thức | Mô tả |
|---|---|
| Tích vô hướng | a.b = |a||b|cos(θ) |
| Tích có hướng | [a,b] = |a||b|sin(θ)n |