Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hai hình bình hành. Hãy vẽ một đường thẳng chia mỗi hình bình hành đó thành hai hình bằng nhau
Đề bài
Cho hai hình bình hành. Hãy vẽ một đường thẳng chia mỗi hình bình hành đó thành hai hình bằng nhau
Lời giải chi tiết
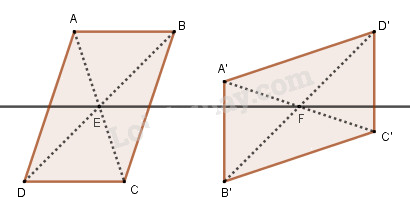
Một đường thẳng đi qua tâm O của hình bình hành thì chia hình bình hành đó thành hai phần bằng nhau, vì phép đối xứng qua tâm O sẽ biến phần này thành phần kia.
Bởi vậy, nếu cho hai hình bình hành, ta chỉ cần vẽ đường thẳng đi qua tâm của hai bình hành này thì đường thẳng đó sẽ chia mỗi hình bình hành thành hai phần bằng nhau.
Nếu tâm hai hình bình hành trùng nhau thì mọi đường thẳng đi qua tâm đó đều chia mỗi hình bình hành thành hai phần bằng nhau
Câu 24 trang 23 SGK Hình học 11 Nâng cao thuộc chương trình học Hình học lớp 11, tập trung vào việc củng cố kiến thức về vectơ và ứng dụng của chúng trong giải quyết các bài toán hình học. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Trước khi bắt tay vào giải, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Thông thường, đề bài sẽ cung cấp một hình vẽ hoặc một mô tả về các điểm, đường thẳng, hoặc các yếu tố hình học khác. Dựa vào đó, chúng ta cần:
(Giả sử đề bài là: Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng: 2MA2 + AB2 + AC2 = 3BC2)
Lời giải:
Gọi A(xA, yA), B(xB, yB), C(xC, yC). Vì M là trung điểm của BC, ta có:
M( (xB + xC)/2, (yB + yC)/2)
Ta có:
Thay các biểu thức trên vào vế trái của đẳng thức cần chứng minh, ta được:
2MA2 + AB2 + AC2 = 2(((xA - (xB + xC)/2)2 + (yA - (yB + yC)/2)2) + (xA - xB)2 + (yA - yB)2 + (xA - xC)2 + (yA - yC)2
Sau khi khai triển và rút gọn, ta sẽ thu được:
2MA2 + AB2 + AC2 = 3BC2
Vậy, đẳng thức được chứng minh.
Vectơ là một công cụ mạnh mẽ trong việc giải quyết các bài toán hình học. Chúng có thể được sử dụng để:
Hy vọng với lời giải chi tiết và những lưu ý trên, bạn đã hiểu rõ cách giải Câu 24 trang 23 SGK Hình học 11 Nâng cao. Hãy luyện tập thêm nhiều bài tập tương tự để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.