Giải Câu 12 Trang 17 SGK Đại số và Giải tích 11 Nâng cao

Câu 12 trang 17 SGK Đại số và Giải tích 11 Nâng cao

Câu 12 trang 17 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng trong chương trình học.

Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, đồ thị hàm số và các phép biến đổi hàm số để giải quyết.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin làm bài tập.

a. Từ đồ thị của hàm số y = cosx, hãy suy ra đồ thị của các hàm số sau và vẽ đồ thị của các hàm số đó :

LG a

Từ đồ thị của hàm số \(y = \cos x\), hãy suy ra đồ thị của các hàm số sau và vẽ đồ thị của các hàm số đó:

\(y = \cos x + 2\)

\(y = \cos \left( {x - {\pi \over 4}} \right)\)

Phương pháp giải:

Sử dụng lý thuyết tịnh tiến đồ thị:

Cho hàm số y=f(x) có đồ thị (C). Khi đó,

+) Hàm số y=f(x)+p có được do tịnh tiến (C) lên trên p đơn vị (p > 0)

+) Hàm số y=f(x-q) có được do tịnh tiến (C) sang phải q đơn vị (q > 0)

Lời giải chi tiết:

Đồ thị của hàm số \(y = \cos x + 2\) có được do tịnh tiến đồ thị của hàm số \(y = \cos x\) lên trên một đoạn có độ dài bằng \(2\)

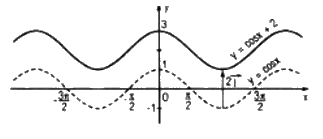
Câu 12 trang 17 SGK Đại số và Giải tích 11 Nâng cao 1

Đồ thị của hàm số \(y = \cos \left( {x - {\pi \over 4}} \right)\) có được do tịnh tiến đồ thị của hàm số y = cosx sang phải một đoạn có độ dài \({\pi \over 4}\)

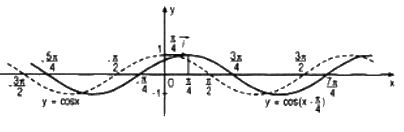
Câu 12 trang 17 SGK Đại số và Giải tích 11 Nâng cao 2

LG b

Hỏi mỗi hàm số đó có phải là hàm số tuần hoàn không ?

Lời giải chi tiết:

Các hàm số trên đều là hàm tuần hoàn vì:

nếu \(f(x) = \cos x + 2\) thì \(f(x + 2π) = \cos(x + 2π) + 2\)

\(= \cos x + 2 = f(x), ∀x \in\mathbb R\)

Và nếu \(g(x) = \cos \left( {x - {\pi \over 4}} \right)\) thì:

\(g(x + 2π) = \cos \left( {x + 2\pi - {\pi \over 4}} \right)\)

\(=\cos \left( {x - {\pi \over 4}} \right) = g\left( x \right)\) , \(∀x \in\mathbb R\)

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Câu 12 trang 17 SGK Đại số và Giải tích 11 Nâng cao – hành trang không thể thiếu trong chuyên mục Bài tập Toán lớp 11 trên nền tảng đề thi toán. Bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải Chi Tiết Câu 12 Trang 17 SGK Đại số và Giải tích 11 Nâng cao

Câu 12 trang 17 SGK Đại số và Giải tích 11 Nâng cao thuộc chương trình học kỳ I, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc hai. Bài tập này thường yêu cầu học sinh xác định các yếu tố của hàm số, vẽ đồ thị và tìm các điểm đặc biệt của đồ thị.

Nội Dung Bài Tập

Thông thường, câu 12 trang 17 sẽ đưa ra một hàm số bậc hai có dạng y = ax² + bx + c và yêu cầu:

Xác định hệ số a, b, c.
Tìm tọa độ đỉnh của parabol.
Tìm trục đối xứng của parabol.
Xác định khoảng đồng biến, nghịch biến của hàm số.
Vẽ đồ thị hàm số.
Tìm giá trị lớn nhất hoặc nhỏ nhất của hàm số.

Phương Pháp Giải

Để giải quyết bài tập này một cách hiệu quả, bạn cần nắm vững các kiến thức sau:

Công thức tính tọa độ đỉnh: x_đỉnh = -b/2a, y_đỉnh = -Δ/4a (với Δ = b² - 4ac).
Phương trình trục đối xứng: x = -b/2a.
Xác định khoảng đồng biến, nghịch biến:
- Nếu a > 0: Hàm số nghịch biến trên (-∞; -b/2a) và đồng biến trên (-b/2a; +∞).
- Nếu a < 0: Hàm số đồng biến trên (-∞; -b/2a) và nghịch biến trên (-b/2a; +∞).
Cách vẽ đồ thị: Xác định các điểm đặc biệt như đỉnh, giao điểm với trục hoành (nếu có), giao điểm với trục tung và một vài điểm khác để vẽ đồ thị chính xác.

Ví Dụ Minh Họa

Bài tập: Cho hàm số y = 2x² - 8x + 6. Hãy xác định tọa độ đỉnh, trục đối xứng và vẽ đồ thị hàm số.

Giải:

Hệ số: a = 2, b = -8, c = 6.
Tọa độ đỉnh: x_đỉnh = -(-8)/(2*2) = 2, y_đỉnh = -((-8)² - 4*2*6)/(4*2) = -1. Vậy tọa độ đỉnh là (2; -1).
Trục đối xứng: x = 2.
Giao điểm với trục tung: x = 0 => y = 6. Vậy giao điểm là (0; 6).
Giao điểm với trục hoành: y = 0 => 2x² - 8x + 6 = 0 => x² - 4x + 3 = 0. Giải phương trình bậc hai, ta được x₁ = 1, x₂ = 3. Vậy giao điểm là (1; 0) và (3; 0).

Dựa vào các điểm đã xác định, ta có thể vẽ được đồ thị hàm số.

Lưu Ý Quan Trọng

Khi giải bài tập về hàm số bậc hai, bạn cần chú ý:

Kiểm tra kỹ các hệ số a, b, c.
Sử dụng đúng công thức tính tọa độ đỉnh và trục đối xứng.
Vẽ đồ thị chính xác để có thể đọc được các thông tin về hàm số.
Luyện tập thường xuyên để nắm vững kiến thức và kỹ năng giải bài tập.

Ứng Dụng Thực Tế

Hàm số bậc hai có nhiều ứng dụng trong thực tế, ví dụ như:

Tính quỹ đạo của vật ném.
Xác định hình dạng của các cầu, vòm.
Mô tả sự thay đổi của các đại lượng vật lý.

Tổng Kết

Câu 12 trang 17 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng giúp bạn củng cố kiến thức về hàm số bậc hai. Hy vọng với lời giải chi tiết và phương pháp giải hiệu quả mà chúng tôi cung cấp, bạn sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn học.