Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Hình học 11 Nâng cao.
Trong bài viết này, chúng tôi sẽ cùng nhau giải quyết Câu 6 trang 125 SGK Hình học 11 Nâng cao, giúp bạn hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Hãy cùng bắt đầu với lời giải chi tiết và những lưu ý quan trọng nhé!
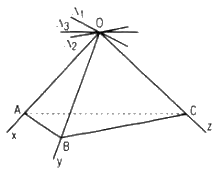
Cho ba tia Ox, Oy, Oz không đồng phẳng. Chứng minh rằng các tia phân giác ngoài của các góc xOy, yOz và zOx đồng phẳng .
Đề bài
Cho ba tia Ox, Oy, Oz không đồng phẳng. Chứng minh rằng các tia phân giác ngoài của các góc xOy, yOz và zOx đồng phẳng .
Lời giải chi tiết
Giả sử Δ1, Δ2, Δ3 lần lượt là ba đường phân giác ngoài của các góc xOy, yOz, xOz. Nếu trên các tia Ox, Oy, Oz lần lượt lấy các điểm A, B, C sao cho OA = OB = OC thì dễ thấy Δ1 // AB, Δ2 // BC, Δ3 // CA.
Vậy Δ1, Δ2, Δ3 đồng phẳng
Câu 6 trang 125 SGK Hình học 11 Nâng cao yêu cầu chúng ta vận dụng kiến thức về đường thẳng vuông góc với mặt phẳng để giải quyết một bài toán cụ thể. Bài toán thường liên quan đến việc chứng minh tính vuông góc, xác định góc giữa đường thẳng và mặt phẳng, hoặc tính khoảng cách.
Trước khi bắt đầu giải, điều quan trọng là phải đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu cần tìm. Thông thường, đề bài sẽ cung cấp thông tin về một hình chóp hoặc một hình đa diện, và yêu cầu chúng ta chứng minh một mối quan hệ hình học nào đó.
Để giải quyết bài toán này, chúng ta cần nắm vững các định nghĩa và tính chất sau:
(Giả sử đề bài cụ thể là: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt đáy. Gọi M là trung điểm của CD. Chứng minh rằng SM vuông góc với mặt phẳng (ABCD).)
Ngoài bài toán trên, còn rất nhiều dạng bài tập tương tự liên quan đến đường thẳng vuông góc với mặt phẳng. Một số dạng bài tập phổ biến bao gồm:
Để giải quyết các dạng bài tập này, chúng ta cần:
Để củng cố kiến thức và kỹ năng giải bài tập, bạn nên luyện tập thêm với các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Hãy chú trọng vào việc hiểu rõ bản chất của bài toán và áp dụng các kiến thức đã học một cách linh hoạt.
Câu 6 trang 125 SGK Hình học 11 Nâng cao là một bài tập quan trọng giúp chúng ta hiểu rõ về đường thẳng vuông góc với mặt phẳng. Bằng cách nắm vững các kiến thức và phương pháp giải đã trình bày, bạn có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Hình học.
Hy vọng bài giải chi tiết này sẽ giúp ích cho bạn trong quá trình học tập. Chúc bạn thành công!