Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, đạo hàm để giải quyết các vấn đề thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin làm bài.
Đồ thị (P) của một hàm số bậc hai
Đề bài
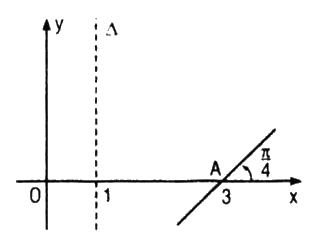
Đồ thị (P) của một hàm số bậc hai y = P(x) đã bị xóa đi, chỉ còn lại trục đối xứng ∆, điểm A thuộc (P) và tiếp tuyến tại A của (P) (h. 5.8). Hãy tìm P(x) và vẽ lại đồ thị (P).
Lời giải chi tiết
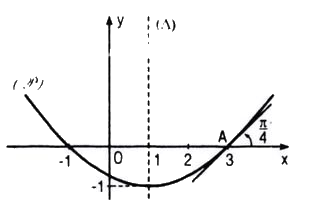
Đa thức phải tìm có dạng : \(P\left( x \right) = a{x^2} + bx + c\,\left( {a \ne 0} \right)\)
Ta có: \(P'\left( x \right) = 2ax + b\)
Vì trục đối xứng (∆) có phương trình x = 1 nên : \( - {b \over {2a}} = 1\,\,\left( 1 \right)\)
Vì đồ thị (P) đi qua điểm A(3 ; 0) nên ta có P(3) = 0, tức là:
\(9a + 3b + c = 0\,\,\left( 2 \right)\)
Vì hệ số góc của tiếp tuyến tại điểm A(3 ; 0) bằng \(\tan {\pi \over 4}\) nên ta có \(P’(3) = 1\), tức là :
\(6a + b = 1\,\left( 3 \right)\)
Giải hệ ba phương trình (1), (2) và (3) với ba ẩn số a, b và c, ta được :
\(\eqalign{ & a = {1 \over 4} \cr & b = - {1 \over 2} \cr & c = - {3 \over 4} \cr} \)
Vậy \(P\left( x \right) = {1 \over 4}{x^2} - {1 \over 2}x - {3 \over 4}\)
Câu 55 trang 221 SGK Đại số và Giải tích 11 Nâng cao thuộc chương trình học lớp 11, tập trung vào việc ứng dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến hàm số. Bài toán này thường yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm, và khả năng vận dụng chúng vào việc tìm cực trị, khoảng đơn điệu của hàm số.
(Đề bài cụ thể sẽ được chèn vào đây. Ví dụ: Cho hàm số y = f(x) = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.)
Để giải quyết bài toán này, chúng ta cần thực hiện các bước sau:
Bước 1: Tính đạo hàm bậc nhất
f'(x) = 3x2 - 6x
Bước 2: Tìm các điểm làm đạo hàm bậc nhất bằng 03x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
Bước 3: Khảo sát dấu của đạo hàm bậc nhất| Khoảng | x < 0 | 0 < x < 2 | x > 2 |
|---|---|---|---|
| f'(x) | + | - | + |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2.
Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.
Để hiểu sâu hơn về bài toán này, bạn có thể thực hành với các bài tập tương tự, thay đổi hàm số và các điều kiện khác. Việc luyện tập thường xuyên sẽ giúp bạn nắm vững kiến thức và kỹ năng giải quyết các bài toán về đạo hàm một cách hiệu quả.
Hy vọng với lời giải chi tiết này, bạn đã hiểu rõ cách giải Câu 55 trang 221 SGK Đại số và Giải tích 11 Nâng cao. Chúc bạn học tập tốt!