Giải Câu 24 Trang 111 SGK Hình Học 11 Nâng Cao

Câu 24 trang 111 SGK Hình học 11 Nâng cao

Câu 24 trang 111 SGK Hình học 11 Nâng cao là một bài tập quan trọng trong chương trình Hình học 11 Nâng cao.

Bài tập này thường yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ, và các tính chất hình học để giải quyết.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và SA ⊥ (ABCD), SA = x. Xác định x để hai mặt phẳng (SBC) và (SDC) tạo với nhau góc 60˚.

Đề bài

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và SA ⊥ (ABCD), SA = x. Xác định x để hai mặt phẳng (SBC) và (SDC) tạo với nhau góc 60˚.

Lời giải chi tiết

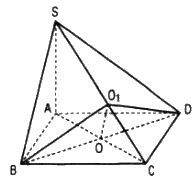
Gọi O là giao điểm của AC và BD. Trong mặt phẳng (SAC) kẻ OO₁ vuông góc với SC.

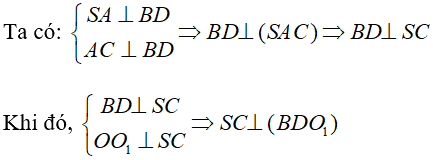
Câu 24 trang 111 SGK Hình học 11 Nâng cao 2

Vậy góc giữa hai mp(SBC) và (SDC) bằng góc giữa hai đường thẳng BO₁ và DO₁.

Mặt khác OO₁ ⊥ BD, OO₁ < OC (vì OC là cạnh huyền của \(\Delta O{O_1}C\) vuông tại O1) mà OC = OB nên \(\widehat {B{O_1}O} > 45^\circ .\)

Tương tự \(\widehat {D{O_1}O} > 45^\circ \) tức \(\widehat {B{O_1}D} >90^\circ \)

Như vậy hai mặt phẳng (SBC) và (SDC) tạo với nhau góc \(60^\circ \) khi và chỉ khi:

\(\widehat {B{O_1}D} =120^\circ \) \( \Leftrightarrow\) \(\widehat {B{O_1}O} = 60^\circ \) (vì ΔBO₁D cân tại O₁)

\( \Leftrightarrow BO = O{O_1}\tan 60^\circ \) \(\Leftrightarrow BO = O{O_1}\sqrt 3 \)

Ta có \(O{O_1} \bot SC\) nên \(\widehat {O{O_1}C} = {90^0}\)

Xét tam giác \(CO{O_1}\) vuông tại \({O_1}\) có:

\(O{O_1} = OC\sin \widehat {OC{O_1}} = OC\sin \widehat {ACS}\) \( = OC.{{SA} \over {SC}}\)

Như vậy : \(BO = O{O_1}\sqrt 3 \Leftrightarrow BO = \sqrt 3 .OC.{{SA} \over {SC}} \) \(\Leftrightarrow SC = \sqrt 3 .SA\)

\( \Leftrightarrow \sqrt {{x^2} + 2{a^2}} = \sqrt 3 .x \Leftrightarrow x = a\)

Vậy khi x = a thì hai mặt phẳng (SBC) và (SDC) tạo với nhau góc 60˚

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Câu 24 trang 111 SGK Hình học 11 Nâng cao – hành trang không thể thiếu trong chuyên mục Giải bài tập Toán 11 trên nền tảng tài liệu toán. Bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải Chi Tiết Câu 24 Trang 111 SGK Hình Học 11 Nâng Cao

Câu 24 trang 111 SGK Hình học 11 Nâng cao thường thuộc vào các chủ đề về vectơ trong không gian, đặc biệt là các bài toán liên quan đến chứng minh đẳng thức vectơ, tìm điểm thỏa mãn điều kiện vectơ, hoặc tính độ dài vectơ. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản sau:

Các định nghĩa về vectơ: Vectơ là gì, các yếu tố của vectơ, hai vectơ bằng nhau.
Các phép toán vectơ: Phép cộng, phép trừ, phép nhân với một số thực.
Các tính chất của phép toán vectơ: Tính giao hoán, tính kết hợp, tính chất phân phối.
Biểu diễn vectơ trong hệ tọa độ: Cách xác định tọa độ của vectơ, các phép toán vectơ trong hệ tọa độ.
Ứng dụng của vectơ trong hình học: Chứng minh các tính chất hình học, giải các bài toán về hình học phẳng và không gian.

Phân Tích Bài Toán Câu 24 Trang 111

Trước khi bắt tay vào giải bài toán, điều quan trọng là phải đọc kỹ đề bài, xác định rõ yêu cầu của bài toán, và phân tích các dữ kiện đã cho. Thông thường, bài toán sẽ cung cấp một số thông tin về các điểm, các vectơ, hoặc các mối quan hệ giữa chúng. Dựa vào các thông tin này, học sinh cần tìm ra cách tiếp cận phù hợp để giải quyết bài toán.

Phương Pháp Giải Bài Toán Vectơ

Có nhiều phương pháp khác nhau để giải các bài toán về vectơ, tùy thuộc vào từng bài toán cụ thể. Một số phương pháp thường được sử dụng bao gồm:

Phương pháp hình học: Sử dụng các tính chất hình học để chứng minh đẳng thức vectơ hoặc tìm điểm thỏa mãn điều kiện vectơ.
Phương pháp tọa độ: Sử dụng hệ tọa độ để biểu diễn các vectơ và thực hiện các phép toán vectơ.
Phương pháp biến đổi tương đương: Sử dụng các tính chất của phép toán vectơ để biến đổi biểu thức vectơ về dạng đơn giản hơn.
Phương pháp quy đồng mẫu số: Áp dụng khi làm việc với các biểu thức vectơ chứa phân số.

Ví Dụ Giải Chi Tiết (Giả định một dạng bài tập phổ biến)

Giả sử bài toán Câu 24 trang 111 SGK Hình học 11 Nâng cao có nội dung như sau:

Cho hình bình hành ABCD. Gọi M là trung điểm của cạnh BC. Chứng minh rằng: overrightarrow{AM} = (1/2)overrightarrow{AB} +overrightarrow{AD}

Lời giải:

Ta có: overrightarrow{AM} =overrightarrow{AB} +overrightarrow{BM}

Vì M là trung điểm của BC nên overrightarrow{BM} = (1/2)overrightarrow{BC}

Mà overrightarrow{BC} =overrightarrow{AD} (do ABCD là hình bình hành)

Do đó, overrightarrow{BM} = (1/2)overrightarrow{AD}

Thay vào biểu thức overrightarrow{AM} ta được: overrightarrow{AM} =overrightarrow{AB} + (1/2)overrightarrow{AD}

Luyện Tập Thêm

Để củng cố kiến thức và kỹ năng giải bài toán về vectơ, học sinh nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Ngoài ra, việc tìm hiểu các ứng dụng của vectơ trong các lĩnh vực khác như vật lý, kỹ thuật cũng sẽ giúp học sinh hiểu sâu hơn về vectơ và tầm quan trọng của nó.

Lời Khuyên Khi Giải Bài Toán Vectơ

Luôn vẽ hình minh họa để hình dung rõ bài toán.
Sử dụng các tính chất của phép toán vectơ một cách linh hoạt.
Kiểm tra lại kết quả sau khi giải xong bài toán.
Tham khảo các lời giải mẫu và học hỏi kinh nghiệm từ những người khác.

Hy vọng với lời giải chi tiết và các phương pháp giải bài toán vectơ được trình bày ở trên, các bạn học sinh sẽ tự tin hơn khi đối mặt với Câu 24 trang 111 SGK Hình học 11 Nâng cao và các bài tập tương tự.