Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, đạo hàm để giải quyết các vấn đề thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin làm bài.
Tìm đạo hàm của mỗi hàm số sau
\(y = {\left( {x - {x^2}} \right)^{32}}\)
Phương pháp giải:
Công thức \(\left( {{u^n}} \right)' = n{u^{n - 1}}u'\)
Lời giải chi tiết:
y' = 32.(x- x2)31.(x - x2)'
= 32(x - x2)31.(1 - 2x)
Vậy \(y' = 32{\left( {x - {x^2}} \right)^{31}}\left( {1 - 2x} \right)\)
\(y = {1 \over {x\sqrt x }}\)
Phương pháp giải:
Sử dụng công thức \(\left( {\frac{1}{u}} \right)' = \frac{{ - u'}}{{{u^2}}}\)
Lời giải chi tiết:
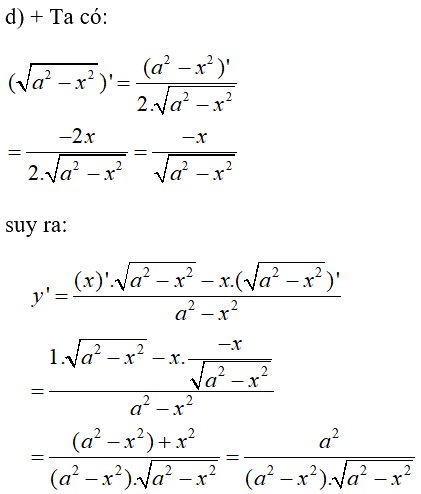
\( \Rightarrow \left( {\frac{1}{{x\sqrt x }}} \right)' = \frac{{ - \left( {x\sqrt x } \right)'}}{{{{\left( {x\sqrt x } \right)}^2}}} \) \(= \frac{{ - \frac{{3\sqrt x }}{2}}}{{{x^2}.x}} = - \frac{3}{{2{x^2}\sqrt x }}\)
\(y' = {{ - 3} \over {2{x^2}\sqrt x }}\)
\(y = {{1 + x} \over {\sqrt {1 - x} }}\)
Phương pháp giải:
Công thức đạo hàm của một thương: \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{{v^2}}}\)
Lời giải chi tiết:
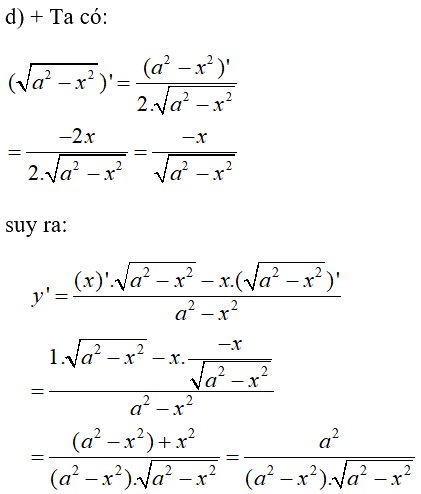
\(y' = {{3 - x} \over {2\sqrt {{{\left( {1 - x} \right)}^3}} }}\)
\(y = {x \over {\sqrt {{a^2} - {x^2}} }}\) (a là hằng số)
Phương pháp giải:
Công thức đạo hàm của một thương: \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{{v^2}}}\).
Lời giải chi tiết:
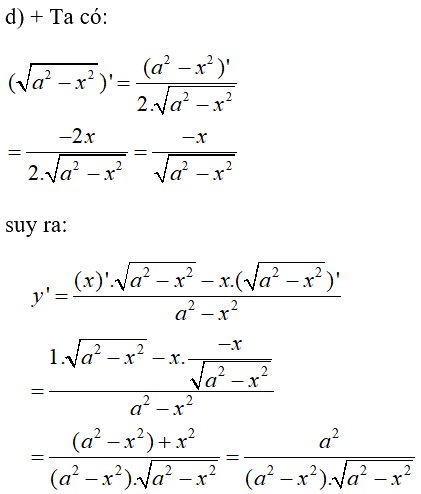
\(\eqalign{ & y' = {{{a^2}} \over {\sqrt {{{\left( {{a^2} - {x^2}} \right)}^3}} }} \cr} \)
Câu 19 trang 204 SGK Đại số và Giải tích 11 Nâng cao thuộc chương trình học lớp 11, tập trung vào việc ứng dụng đạo hàm để khảo sát hàm số. Bài toán này thường yêu cầu học sinh xác định các điểm cực trị, khoảng đồng biến, nghịch biến và vẽ đồ thị hàm số. Dưới đây là lời giải chi tiết:
Trước khi đi vào giải, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu. Thông thường, đề bài sẽ cho một hàm số và yêu cầu:
Giả sử hàm số được cho là: f(x) = x3 - 3x2 + 2
Hàm số f(x) = x3 - 3x2 + 2 là một hàm đa thức, do đó tập xác định của hàm số là D = ℝ.
f'(x) = 3x2 - 6x
Để tìm các điểm cực trị, ta giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
Ta xét dấu của f'(x) trên các khoảng:
Tại x = 0, f'(x) đổi dấu từ dương sang âm, nên hàm số đạt cực đại tại x = 0. Giá trị cực đại là f(0) = 2.
Tại x = 2, f'(x) đổi dấu từ âm sang dương, nên hàm số đạt cực tiểu tại x = 2. Giá trị cực tiểu là f(2) = -2.
Dựa vào các thông tin đã tìm được, ta có thể vẽ đồ thị hàm số f(x) = x3 - 3x2 + 2. Đồ thị hàm số có cực đại tại điểm (0; 2) và cực tiểu tại điểm (2; -2).
Khi giải các bài tập về khảo sát hàm số bằng đạo hàm, cần lưu ý những điều sau:
Việc giải các bài tập về khảo sát hàm số bằng đạo hàm có nhiều ứng dụng trong thực tế, như:
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự trong SGK Đại số và Giải tích 11 Nâng cao hoặc các tài liệu tham khảo khác.
Hy vọng lời giải chi tiết này sẽ giúp bạn hiểu rõ hơn về Câu 19 trang 204 SGK Đại số và Giải tích 11 Nâng cao. Chúc bạn học tốt!