Chương III Hình học 11 Nâng cao tập trung vào kiến thức về đường thẳng và mặt phẳng trong không gian. Để giúp các em học sinh ôn tập và củng cố kiến thức một cách hiệu quả, giaitoan.edu.vn cung cấp bộ câu hỏi trắc nghiệm ôn tập chương III trang 122 SGK Hình học 11 Nâng cao.
Các câu hỏi trắc nghiệm này được biên soạn bám sát nội dung SGK, bao gồm các dạng bài tập khác nhau, từ cơ bản đến nâng cao, giúp các em làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải nhanh các bài toán.
Chọn đáp án đúng:
Cho tứ diện ABCD có trọng tâm G. Mệnh đề nào sau đây là sai ?
A. \(\overrightarrow {OG} = {1 \over 4}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} } \right)\)
B. \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \)
C. \(\overrightarrow {AG} = {2 \over 3}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)\)
D. \(\overrightarrow {AG} = {1 \over 4}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)\)
Giải chi tiết:
(A), (B) đúng.
Gọi G1 là trọng tâm ΔBCD ta có \(\overrightarrow {AG} = {3 \over 4}\overrightarrow {A{G_1}} = {1 \over 4}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)\) nên (D) đúng.
Vậy chọn (C)
Mệnh đề nào sau đây là đúng ?
A. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau ;
B. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau ;
C. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia ;
D. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau thì song song với đường thẳng còn lại.
Giải chi tiết:
Chọn (C)
Cho hai đường thẳng phân biệt a, b và mặt phẳng (P), trong đó a ⊥ (P). Mệnh đề nào sau đây là sai ?
A. Nếu b // (P) thì b ⊥ a
B. Nếu b ⊥ (P) thì b // a
C. Nếu b // a thì b ⊥ (P)
D. Nếu b ⊥ a thì b // (P)
Giải chi tiết:
Nếu b ⊥ a thì có thể b ⊂ (P)
Chọn (D)
Tìm mệnh đề đúng trong các mệnh đề sau :
A. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song ;
B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song ;
C. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song ;
D. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
Giải chi tiết:

\(\left\{ {\matrix{ {(P) \ne (Q)} \cr {(P) \bot a} \cr {(Q) \bot a} \cr } } \right. \Rightarrow (P)//(Q)\)
Chọn (C)
Mệnh đề nào sau đây là đúng ?
A. Hai đường thẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này sẽ vuông góc với mặt phẳng kia ;
B. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau ;
C. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau ;
D. Ba mệnh đề trên đều sai.
Giải chi tiết:
Chọn D.
(A). Sai theo hình vẽ bên

\(\left\{ {\matrix{ {(P) \bot (Q)} \cr {a \subset (Q)} \cr } } \right.\) nhưng a // (P)
(B), (C) sai theo hình vẽ sau.
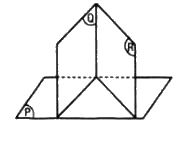
Trong các mệnh đề sau, mệnh đề nào đúng ?
A. Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước ;
B. Có duy nhất một mặt phẳng đi qua một đường thẳng cho trước và vuông góc với một mặt phẳng cho trước ;
C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước ;
D. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
Giải chi tiết:
Chọn (D)

Tìm mệnh đề đúng trong các mệnh đề sau :
A. Nếu hình hộp có hai mặt là hình chữ nhật thì nó là hình hộp chữ nhật ;
B. Nếu hình hộp có ba mặt là hình chữ nhật thì nó là hình hộp chữ nhật ;
C. Nếu hình hộp có bốn mặt là hình chữ nhật thì nó là hình hộp chữ nhật ;
D. Nếu hình hộp có năm mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
Giải chi tiết:
Chọn (D)
Trong các mệnh đề sau, mệnh đề nào đúng ?
A. Nếu hình hộp có hai mặt là hình vuông thì nó là hình lập phương ;
B. Nếu hình hộp có ba mặt chung một đỉnh là hình vuông thì nó là hình lập phương ;
C. Nếu hình hộp có sáu mặt bằng nhau thì nó là hình lập phương ;
D. Nếu hình hộp có bốn đường chéo bằng nhau thì nó là hình lập phương .
Giải chi tiết:
Chọn (B)
Cho hình chóp S.ABC có đáy là tam giác đều. Tìm mệnh đề đúng trong các mệnh đề sau :
A. S.ABC là hình chóp đều nếu các mặt bên của nó là tam giác cân ;
B. S.ABC là hình chóp đều nếu các mặt bên của nó là tam giác cân với đỉnh S ;
C. S.ABC là hình chóp đều nếu góc giữa các mặt phẳng chứa các mặt bên và mặt phẳng chứa đáy bằng nhau ;
D. S.ABC là hình chóp đều nếu các mặt bên có diện tích bằng nhau.
Giải chi tiết:
Chọn (B)
Tìm mệnh đề đúng trong các mệnh đề sau :
A. Đường vuông góc chung của hai đường thẳng chéo nhau thì nằm trong mặt phẳng chứa đường thẳng này và vuông góc với đường thẳng kia ;
B. Đường vuông góc chung của hai đường thẳng chéo nhau thì vuông góc với mặt phẳng chứa đường thẳng này và song song với đường thẳng kia ;
C. Một đường thẳng là đường vuông góc chung của hai đường thẳng chéo nhau nếu nó vuông góc với cả hai đường thẳng đó ;
D. Các mệnh đề trên đều sai.
Giải chi tiết:
Chọn (B)

Hình tứ diện ABCD có AB, AC, AD đôi một vuông góc là AB = AC = AD = 3.
Diện tích tam giác BCD bằng
A. \({{9\sqrt 3 } \over 2}\)
B. \({{9\sqrt 2 } \over 3}\)
C. 27
D. \({{27} \over 2}\)
Giải chi tiết:
Chọn (A).

Ta có: BC = CD = BD = \(3\sqrt 2 \)
Tam giác BCD đều cạnh \(a = 3\sqrt 2 \) nên
\({S_{BCD}} = {{{a^2}\sqrt 3 } \over 4} = {{18\sqrt 3 } \over 4} = {{9\sqrt 3 } \over 2}\)
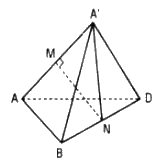
Hình hộp ABCD.A’B’C’D’ có AB = AA’ = AD = a và \(\widehat {A'AB} = \widehat {A'AD} = \widehat {BAD} = 60^\circ .\) Khi đó, khoảng cách giữa các đường thẳng chứa các cạnh đối diện của tứ diện AA’BD bằng :
A. \({{a\sqrt 2 } \over 2}\)
B. \({{a\sqrt 3 } \over 2}\)
C. \(a\sqrt 2 \)
D. \({{3a} \over 2}\)
Giải chi tiết:
Chọn (A)

Tứ diện A’ABD là tứ diện đều cạnh a.
M, N lần lượt là trung điểm AA’, BD.
MN là đoạn vuông góc chung của AA’ và BD. Ta có:
\(M{N^2} = A'{N^2} - A'{M^2}\)
\(= {\left( {{{a\sqrt 3 } \over 2}} \right)^2} - {\left( {{a \over 2}} \right)^2}\)
\(= {{3{a^2}} \over 4} - {{{a^2}} \over 4} = {{{a^2}} \over 2} \)
\(\Rightarrow {\rm M}{\rm N} = {{a\sqrt 2 } \over 2}\)
Chương III trong sách giáo khoa Hình học 11 Nâng cao là một phần quan trọng, đặt nền móng cho việc học tập các kiến thức hình học không gian ở các lớp trên. Chương này tập trung vào các khái niệm cơ bản như đường thẳng và mặt phẳng trong không gian, các mối quan hệ song song và vuông góc giữa chúng. Việc nắm vững các khái niệm này là điều kiện tiên quyết để giải quyết các bài toán phức tạp hơn.
Trước khi bắt đầu giải các câu hỏi trắc nghiệm, chúng ta cần ôn lại những kiến thức lý thuyết quan trọng sau:
Các câu hỏi trắc nghiệm ôn tập chương III thường xoay quanh các dạng bài sau:
Dưới đây là giải chi tiết một số câu hỏi trắc nghiệm tiêu biểu trong chương III trang 122 SGK Hình học 11 Nâng cao:
Câu 1: Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa đường thẳng a và song song với đường thẳng b?
A. 0
B. 1
C. Vô số
D. 2
Giải: Theo tính chất của hai đường thẳng chéo nhau, có duy nhất một mặt phẳng chứa đường thẳng a và song song với đường thẳng b. Vậy đáp án là B. 1.
Câu 2: Cho hình chóp S.ABCD. Gọi M là trung điểm của cạnh CD. Khẳng định nào sau đây đúng?
A. SM ⊥ (ABCD)
B. SM ⊥ CD
C. SM ⊥ AM
D. SM ⊥ BC
Giải: Để xác định đáp án đúng, cần phân tích kỹ hình chóp S.ABCD và các mối quan hệ vuông góc. Thông thường, đáp án đúng sẽ liên quan đến tính chất của đường trung tuyến trong tam giác hoặc các yếu tố đặc biệt của hình chóp. (Giải thích chi tiết hơn cần dựa vào hình vẽ cụ thể của hình chóp).
Hy vọng với bộ câu hỏi trắc nghiệm ôn tập chương III trang 122 SGK Hình học 11 Nâng cao này, các em học sinh sẽ có thêm công cụ để ôn tập và củng cố kiến thức, đạt kết quả tốt trong các kỳ thi sắp tới.