Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác các bài tập trong sách giáo khoa Hình học 11 Nâng cao. Bài viết này sẽ hướng dẫn bạn giải quyết hoàn toàn Câu 30 trang 117 SGK Hình học 11 Nâng cao một cách dễ hiểu nhất.
Chúng tôi luôn cố gắng mang đến những phương pháp giải toán hiệu quả, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh đều bằng a. Góc tạo bởi cạnh bên và mặt đáy bằng 30˚. Hình chiếu H của điểm A trên mặt phẳng (A’B’C’) thuộc đường thẳng B’C’.
Đề bài
Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh đều bằng a. Góc tạo bởi cạnh bên và mặt đáy bằng 30˚. Hình chiếu H của điểm A trên mặt phẳng (A’B’C’) thuộc đường thẳng B’C’.
a. Tính khoảng cách giữa hai mặt phẳng đáy
b. Chứng minh rằng hai đường thẳng AA’ và B’C’ vuông góc, tính khoảng cách giữa chúng.
Lời giải chi tiết
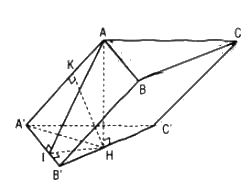
Ta có: AH ⊥ (A’B’C’) nên \(\widehat {AA'H}\) là góc giữa AA’ và mp(A’B’C’) do đó \(\widehat {AA'H} = 30^\circ \)
a. Khoảng cách giữa hai mp đáy chính là AH, ta có :
\(AH = AA'\sin 30^\circ = {a \over 2}\)
b. Tam giác AHA’ vuông tại H nên \(A'H = AA'\cos 30^\circ = {{a\sqrt 3 } \over 2}.\) Vì A’B’C’ là tam giác đều cạnh a, H thuộc đường thẳng B’C’ mà \(A'H = {{a\sqrt 3 } \over 2}\) nên A’H ⊥ B’C’ và H là trung điểm B’C’.
Mặt khác, AH ⊥ B’C’ nên AA’ ⊥ B’C’. Kẻ đường cao HK của tam giác AA’H thì HK chính là khoảng cách giữa AA’ và B’C’. Do AA’.HK = AH.A’H nên \(HK = {{{a \over 2}.{{a\sqrt 3 } \over 2}} \over a} = {{a\sqrt 3 } \over 4}\)
Câu 30 trang 117 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về đường thẳng và mặt phẳng trong không gian, đặc biệt là các tính chất liên quan đến quan hệ song song và vuông góc. Bài toán này thường xuất hiện trong các đề thi và kiểm tra, do đó việc hiểu rõ cách giải là vô cùng cần thiết.
Trước khi bắt đầu giải bài toán, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu. Thông thường, đề bài sẽ cho một hình không gian và yêu cầu chứng minh một mối quan hệ nào đó giữa các đường thẳng và mặt phẳng. Việc phân tích đề bài giúp chúng ta xác định được các yếu tố cần thiết để giải quyết bài toán.
Để giải quyết các bài toán về quan hệ song song và vuông góc, chúng ta có thể sử dụng một số phương pháp sau:
(Giả sử đề bài là: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Gọi M là trung điểm của CD. Chứng minh rằng SM vuông góc với mặt phẳng (ABCD).)
Lời giải:
Khi giải các bài toán về quan hệ song song và vuông góc, cần lưu ý một số điểm sau:
Để củng cố kiến thức, bạn có thể làm thêm một số bài tập tương tự sau:
Hy vọng rằng với lời giải chi tiết và các phương pháp giải bài toán được trình bày ở trên, bạn đã hiểu rõ cách giải Câu 30 trang 117 SGK Hình học 11 Nâng cao. Chúc bạn học tập tốt và đạt kết quả cao trong môn Hình học!