Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Hình học 11 Nâng cao. Bài viết này sẽ tập trung vào việc giải Câu 10 trang 13 SGK Hình học 11 Nâng cao, giúp bạn hiểu rõ phương pháp và cách tiếp cận để giải quyết các bài toán tương tự.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng, dễ hiểu và phù hợp với chương trình học hiện hành. Hãy cùng khám phá lời giải chi tiết ngay sau đây!
Cho hai điểm B,C cố định nằm trên đường tròn
Đề bài
Cho hai điểm B,C cố định nằm trên đường tròn và điểm A thay đổi trên đường tròn đó. Hãy dùng phép đối xứng trục để chứng minh rằng trực tâm H của tam giác ABC nằm trên một đường tròn cố định
Hướng dẫn : Khi BC không phải là đường kính, gọi H’ là giao điểm của đường thẳng AH với đường tròn (O; R). Chứng minh rằng H đối xứng với H’ qua đường thẳng BC.
Lời giải chi tiết
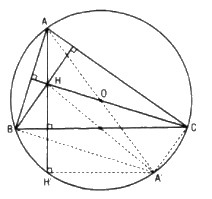
Trường hợp BC là đường kính thì tam giác ABC vuông tại A nên H trùng A
Do đó H nằm trên đường tròn cố định (O ; R)
Xét trường hợp BC không là đường kính.
Giả sử đường thẳng AH cắt đường tròn (O ; R) tại H’.
Gọi AA’ là đường kính của đường tròn (O ; R) thì:
A’B // CH (vì cùng vuông góc với AB)
A’C // BH (vì cùng vuông góc với AC)
Do đó A’BHC là hình bình hành.
Vậy BC đi qua trung điểm của HA’
Mặt khác BC // A’H’ (vì cùng vuông góc với AH) nên BC cũng đi qua trung điểm của HH’
(do BC đi qua trung điểm của HA' và song song A'H' nên đi qua trung điểm của HH')
Do đó H và H’ đối xứng với nhau qua BC.
Nếu gọi Đ là phép đối xứng có trục là đường thẳng BC thì Đ biến H’ thành H.
Nhưng H’ luôn luôn nằm trên (O ; R) nên H nằm trên đường tròn cố định là ảnh của đường tròn (O ; R) qua phép đối xứng trục Đ
Cách khác: Gọi H’ là điểm đối xứng của H qua BC. Chứng minh tứ giác ABH’C nội tiếp, từ đó suy ra H’ nằm trên (O ; R).
Câu 10 trang 13 SGK Hình học 11 Nâng cao thuộc chương trình học về Vectơ trong không gian. Bài toán này thường yêu cầu học sinh vận dụng kiến thức về các phép toán vectơ, đặc biệt là tích vô hướng để chứng minh các mối quan hệ hình học.
Để bắt đầu, chúng ta cần xem xét kỹ đề bài của Câu 10 trang 13 SGK Hình học 11 Nâng cao. Thông thường, bài toán sẽ cho một hình chóp hoặc một tứ diện, và yêu cầu chứng minh một đẳng thức vectơ liên quan đến các vectơ tạo bởi các cạnh hoặc đường cao của hình đó. Ví dụ, bài toán có thể yêu cầu chứng minh rằng một góc giữa hai vectơ bằng 90 độ, hoặc chứng minh rằng hai vectơ cùng phương.
Để giải quyết bài toán này, chúng ta có thể áp dụng các phương pháp sau:
Giả sử đề bài yêu cầu chứng minh rằng hai vectơ a và b vuông góc với nhau. Chúng ta có thể thực hiện như sau:
1. Tính tích vô hướng của a và b: a ⋅ b.
2. Nếu a ⋅ b = 0, thì a và b vuông góc với nhau.
Ngoài việc giải Câu 10 trang 13 SGK Hình học 11 Nâng cao, bạn nên tìm hiểu thêm về các ứng dụng của tích vô hướng trong hình học không gian, chẳng hạn như tính góc giữa hai đường thẳng, tính khoảng cách từ một điểm đến một mặt phẳng, và chứng minh các tính chất của hình chóp và tứ diện.
Để củng cố kiến thức, bạn có thể thử giải các bài tập tương tự trong sách giáo khoa hoặc các tài liệu tham khảo khác. Hãy áp dụng các phương pháp đã học để giải quyết các bài toán một cách hiệu quả.
Câu 10 trang 13 SGK Hình học 11 Nâng cao là một bài toán điển hình để rèn luyện kỹ năng vận dụng kiến thức về vectơ trong không gian. Bằng cách phân tích đề bài, chọn hệ tọa độ phù hợp, biểu diễn các vectơ, tính tích vô hướng và đưa ra kết luận, bạn có thể giải quyết bài toán một cách chính xác và hiệu quả. Chúc bạn học tốt!
| Khái niệm | Giải thích |
|---|---|
| Tích vô hướng | Là một phép toán giữa hai vectơ, cho kết quả là một số thực. |
| Vectơ vuông góc | Hai vectơ vuông góc khi và chỉ khi tích vô hướng của chúng bằng 0. |