Giải Câu 12 Trang 63 SGK Đại số và Giải tích 11 Nâng cao

Câu 12 trang 63 SGK Đại số và Giải tích 11 Nâng cao

Câu 12 trang 63 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng trong chương trình học.

Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, đạo hàm để giải quyết các vấn đề thực tế.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin làm bài.

Xét hồ sơ mạng điện ở hình 2.3 có 6 công tắc khác nhau, trong đó mỗi công tắc có 2 trạng thái đóng và mở.

Đề bài

Xét hồ sơ mạng điện ở hình 2.3 có 6 công tắc khác nhau, trong đó mỗi công tắc có 2 trạng thái đóng và mở.

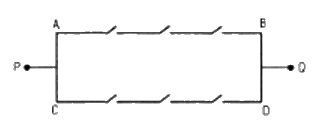
Câu 12 trang 63 SGK Đại số và Giải tích 11 Nâng cao 1

Hỏi có bao nhiêu cách đóng – mở 6 công tắc để mạng điện thông mạch từ P đến Q (tức là có dòng điện từ P đến Q) ?

Lời giải chi tiết

Mỗi cách đóng mở công tắc của mạng điện được gọi là một trạng thái của mạng điện.

Mỗi công tắc có 2 cách đóng mở, mà có 6 công tắc nên theo quy tắc nhân, mạng điện có \(2^6= 64\) trạng thái.

Ta đếm số trạng thái không thông mạch (không có dòng điện đi qua).

Mạch gồm hai nhánh A → B và C → D. Trạng thái không thông mạch xảy ra khi và chỉ khi cả hai nhánh A → B và C → D đều không thông mạch.

Dễ thấy nhánh A → B có \(2^3=8 \) trạng thái trong đó chỉ có duy nhất một trạng thái thông mạch (3 công tắc đều mở), còn lại có 7 trạng thái không thông mạch.

Tương tự ở nhánh C → D có 7 trạng thái không thông mạch.

Theo quy tắc nhân, ta có \(7.7 = 49\) trạng thái mà cả A → B và C → D đều không thông mạch.

Vậy mạng điện có \(64 – 49 = 15\) trạng thái thông mạch từ P tới Q.

Cách khác:

Ta đếm trực tiếp như sau:

TH1: A → B thông mạch, C → D không thông mạch.

Có 1 cách để A → B thông mạch.

Có 7 cách để C → D không thông mạch.

Theo quy tắc nhân có 1.7=7 cách.

TH2: A → B không thông mạch, C → D thông mạch.

Có 7 cách để A → B không thông mạch.

Có 1 cách để C → D thông mạch.

Theo quy tắc nhân có 1.7=7 cách.

TH3: Cả A → B và C → D thông mạch

Có 1.1=1 cách.

Vậy theo quy tắc cộng có 7+7+1=15 cách thông mạch mạng điện.

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Câu 12 trang 63 SGK Đại số và Giải tích 11 Nâng cao – hành trang không thể thiếu trong chuyên mục Học tốt Toán lớp 11 trên nền tảng toán học. Bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải Chi Tiết Câu 12 Trang 63 SGK Đại số và Giải tích 11 Nâng cao

Câu 12 trang 63 SGK Đại số và Giải tích 11 Nâng cao thuộc chương trình học kỳ I, lớp 11. Bài toán này thường liên quan đến việc xét tính đơn điệu của hàm số, tìm cực trị, hoặc giải phương trình, bất phương trình chứa dấu giá trị tuyệt đối. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, các quy tắc tính đạo hàm, và các phương pháp xét tính đơn điệu của hàm số.

Phân Tích Đề Bài

Trước khi bắt đầu giải, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Thông thường, đề bài sẽ yêu cầu chúng ta tìm một giá trị nào đó, chứng minh một bất đẳng thức, hoặc giải một phương trình, bất phương trình. Việc phân tích đề bài một cách cẩn thận sẽ giúp chúng ta lựa chọn phương pháp giải phù hợp.

Phương Pháp Giải

Có nhiều phương pháp khác nhau để giải Câu 12 trang 63 SGK Đại số và Giải tích 11 Nâng cao, tùy thuộc vào dạng bài cụ thể. Một số phương pháp thường được sử dụng bao gồm:

Phương pháp xét dấu: Sử dụng để giải các phương trình, bất phương trình chứa dấu giá trị tuyệt đối.
Phương pháp đạo hàm: Sử dụng để xét tính đơn điệu của hàm số, tìm cực trị.
Phương pháp biến đổi tương đương: Sử dụng để chứng minh các bất đẳng thức.
Phương pháp sử dụng tính chất của hàm số: Sử dụng để giải các bài toán liên quan đến hàm số đặc biệt.

Lời Giải Chi Tiết

Để minh họa, chúng ta sẽ xét một ví dụ cụ thể về Câu 12 trang 63 SGK Đại số và Giải tích 11 Nâng cao. Giả sử đề bài yêu cầu chúng ta tìm giá trị của tham số m để phương trình f(x) = m có nghiệm.

Bước 1: Tính đạo hàm f'(x).
Bước 2: Tìm các điểm cực trị của hàm số f(x) bằng cách giải phương trình f'(x) = 0.
Bước 3: Tính giá trị của hàm số f(x) tại các điểm cực trị.
Bước 4: Dựa vào đồ thị hàm số hoặc các tính chất của hàm số, xác định khoảng giá trị của m để phương trình f(x) = m có nghiệm.

Ví Dụ Minh Họa

Ví dụ: Cho hàm số y = x³ - 3x² + 2. Tìm giá trị của m để phương trình x³ - 3x² + 2 = m có nghiệm.

Lời giải:

Ta có y' = 3x² - 6x. Giải phương trình y' = 0 ta được x = 0 hoặc x = 2.

Hàm số đạt cực đại tại x = 0 với giá trị y = 2 và đạt cực tiểu tại x = 2 với giá trị y = -2.

Vậy, phương trình x³ - 3x² + 2 = m có nghiệm khi -2 ≤ m ≤ 2.

Lưu Ý Quan Trọng

Khi giải Câu 12 trang 63 SGK Đại số và Giải tích 11 Nâng cao, học sinh cần chú ý các điểm sau:

Đọc kỹ đề bài và xác định rõ yêu cầu của bài toán.
Nắm vững các kiến thức cơ bản về đạo hàm, các quy tắc tính đạo hàm, và các phương pháp xét tính đơn điệu của hàm số.
Lựa chọn phương pháp giải phù hợp với từng dạng bài cụ thể.
Kiểm tra lại kết quả sau khi giải xong.

Tổng Kết

Câu 12 trang 63 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số, đạo hàm. Bằng cách nắm vững các kiến thức cơ bản và áp dụng các phương pháp giải phù hợp, học sinh có thể tự tin giải quyết bài toán này một cách hiệu quả. Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.