Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, đạo hàm để giải quyết các vấn đề thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin làm bài.
Cho hình vuông
Đề bài
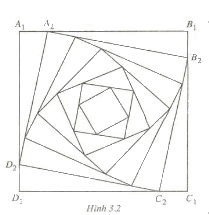
Cho hình vuông A1B1C1D1 có các cạnh bằng 6cm. Người ta dựng các hình vuông A2B2C2D2, A3B3C3D3, …, AnBnCnDn, … theo cách sau : Với mỗi n = 2, 3, 4, … lấy các điểm An, Bn , Cn, và Dn tương ứng trên các cạnh An-1Bn-1, Bn-1Cn-1, Cn-1Dn-1và Dn-1An-1 sao cho An-1An = 1cm và AnBnCnDn là một hình vuông (h.3.2). Xét dãy số (un) với un là độ dài cạnh của hình vuông AnBnCnDn.
Hãy cho dãy số (un) nói trên bởi hệ thức truy hồi.
Lời giải chi tiết
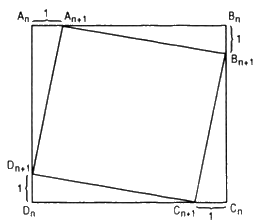
Với mỗi \(n \in \mathbb N^*\), xét các hình vuông \({A_n}{B_n}{C_n}{D_n}\) và \({A_{n + 1}}{B_{n + 1}}{C_{n + 1}}{D_{n + 1}},\) ta có
\(\eqalign{& {u_{n + 1}} = {A_{n + 1}}{B_{n + 1}} \cr&= \sqrt {{{\left( {{A_{n + 1}}{B_n}} \right)}^2} +{{\left( {{B_n}{B_{n + 1}}} \right)}^2}} \cr & = \sqrt {{{\left( {{A_n}{B_n} - 1} \right)}^2} + {1^2}} \cr & = \sqrt {{{\left( {{u_n} - 1} \right)}^2} + 1} \cr} \)
Câu 11 trang 106 trong sách giáo khoa Đại số và Giải tích 11 Nâng cao thường xoay quanh các bài toán liên quan đến đạo hàm của hàm số. Đạo hàm đóng vai trò then chốt trong việc xác định tính đơn điệu, cực trị của hàm số, và là nền tảng cho nhiều ứng dụng trong các lĩnh vực khoa học kỹ thuật. Việc hiểu rõ bản chất của đạo hàm và các quy tắc tính đạo hàm là điều kiện tiên quyết để giải quyết thành công bài toán này.
Trước khi đi vào giải chi tiết, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:
Để giải quyết hiệu quả Câu 11 trang 106, học sinh cần đọc kỹ đề bài, xác định rõ yêu cầu của bài toán. Thông thường, đề bài sẽ yêu cầu:
(Giả sử đề bài là: Cho hàm số y = x3 - 3x2 + 2. Tìm đạo hàm y' và xác định các điểm cực trị của hàm số.)
Bước 1: Tính đạo hàm y'
Sử dụng quy tắc đạo hàm của tổng và lũy thừa, ta có:
y' = 3x2 - 6x
Bước 2: Tìm các điểm cực trịĐể tìm các điểm cực trị, ta giải phương trình y' = 0:
3x2 - 6x = 0
⇔ 3x(x - 2) = 0
⇔ x = 0 hoặc x = 2
Bước 3: Xác định loại cực trịTa xét dấu của y' trên các khoảng xác định:
Vậy, hàm số đạt cực đại tại x = 0, giá trị cực đại là y(0) = 2 và đạt cực tiểu tại x = 2, giá trị cực tiểu là y(2) = -2.
Ngoài Câu 11 trang 106, còn rất nhiều bài tập tương tự trong sách giáo khoa và các đề thi. Để giải tốt các bài tập này, học sinh cần:
Câu 11 trang 106 SGK Đại số và Giải tích 11 Nâng cao là một bài tập điển hình để rèn luyện kỹ năng tính đạo hàm và ứng dụng đạo hàm vào việc giải quyết các bài toán thực tế. Việc nắm vững lý thuyết, luyện tập thường xuyên và áp dụng các mẹo giải sẽ giúp học sinh tự tin chinh phục bài toán này và đạt kết quả tốt trong môn học.