Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hai hình bình hành ABCD VÀ ABEF nằm trong hai mặt phẳng khác nhau. Lấy các điểm M, N lần lượt thuộc các đường chéo AC, BF sao cho MC = 2AM, NF = 2BN. Qua M, N, kẻ các đường thẳng song song với AB cắt các cạnh AD, AF lần lượt tại M1, N1. Chứng minh rằng:
Đề bài
Cho hai hình bình hành ABCD VÀ ABEF nằm trong hai mặt phẳng khác nhau. Lấy các điểm M, N lần lượt thuộc các đường chéo AC, BF sao cho MC = 2AM, NF = 2BN. Qua M, N, kẻ các đường thẳng song song với AB cắt các cạnh AD, AF lần lượt tại M1, N1. Chứng minh rằng:
a. MN // DE
b. M1N1 // mp(DEF)
c. mp(MNN1M1) // mp(DEF)
Lời giải chi tiết
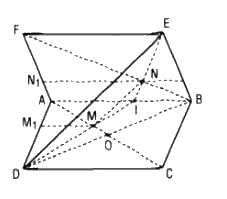
a. Gọi O là tâm hình bình hành ABCD, ta có AO là trung tuyến và \({{AM} \over {AO}} = {{2AM} \over {AC}} = {2 \over 3}\)
⇒ M là trọng tâm của tam giác ABD , tương tự N là trọng tâm tam giác ABE
Gọi I là trung điểm của AB thì M, N lần lượt trên DI và EI
Trong tam giác IDE ta có: \({{IM} \over {ID}} = {{IN} \over {IE}} = {1 \over 3}\) nên MN // DE và \(MN = {1 \over 3}DE\)
b. Trong ∆FAB: NN1 // AB ⇒ \({{A{N_1}} \over {AF}} = {{BN} \over {BF}} = {1 \over 3}\)
Trong ∆DAC: MM1 // CD ⇒ \({{A{M_1}} \over {AD}} = {{AM} \over {AC}} = {1 \over 3}\)
Do đó \({{A{N_1}} \over {AF}} = {{A{M_1}} \over {AD}}\) nên M1N1 // DF
Mà DF ⊂ (DEF) suy ra M1N1 // mp(DEF)
c. Ta có : M1N1 // DF , NN1 // EF
mà M1N1 và NN1 cắt nhau và nằm trong mp(MNN1M1), còn DF và EF cắt nhau và nằm trong mp(DEF)
Vậy mp(MNN1M1) // mp(DEF)
Bài tập Câu 4 trang 78 SGK Hình học 11 Nâng cao thường xoay quanh việc chứng minh đẳng thức vectơ, tìm mối quan hệ giữa các vectơ, hoặc xác định vị trí tương đối của các điểm trong không gian sử dụng vectơ. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản sau:
Để cung cấp một lời giải cụ thể, chúng ta cần biết nội dung chính xác của Câu 4 trang 78. Tuy nhiên, dưới đây là một ví dụ về cách tiếp cận giải một bài tập vectơ điển hình:
Ví dụ: Cho hình bình hành ABCD. Gọi M là trung điểm của BC. Chứng minh rằng AM = 1/2(AB + AC).
AM = AB + 1/2(AC - AB) = AB + 1/2AC - 1/2AB = 1/2AB + 1/2AC = 1/2(AB + AC)
Ngoài dạng bài tập chứng minh đẳng thức vectơ như trên, Câu 4 trang 78 SGK Hình học 11 Nâng cao có thể xuất hiện các dạng bài tập sau:
Để giải các bài tập này, học sinh cần:
Ngoài SGK Hình học 11 Nâng cao, học sinh có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức và kỹ năng giải bài tập:
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Hãy truy cập website của chúng tôi để xem thêm nhiều bài giải chi tiết và tài liệu học tập hữu ích khác.