Bài toán này yêu cầu học sinh vận dụng kiến thức về hàm số, đạo hàm để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin làm bài tập.
Xét mạng đường nối các tỉnh A, B, C, D, E, F, G, trong đó số viết trên một cạch cho biết số con đường nối hai tỉnh nằm ở hai
Đề bài
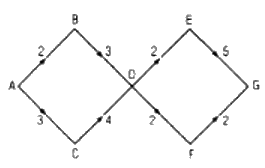
Xét mạng đường nối các tỉnh A, B, C, D, E, F, G, trong đó số viết trên một cạch cho biết số con đường nối hai tỉnh nằm ở haiđầu mút của cạnh (h. 2.2). Hỏi có bao nhiêu cách đi từ tỉnh A đến tỉnh G ?
Phương pháp giải - Xem chi tiết
Liệt kê các trường hợp có thể đi từ A đến G.
Dùng quy tắc nhân đếm số cách đi trong từng TH.
Dùng quy tắc cộng suy ra số cách đi cần tìm.
Lời giải chi tiết
Có 4 phương án đi qua các tỉnh A đến G là :
a. A → B → D → E → G
b. A → B → D → F → G
c. A → C → D → E → G
d. A → C → D → F → G
Theo quy tắc nhân, ta có :
Phương án a: A → B → D → E → G
Có \(2.3.2.5 = 60\) cách đi;
Phương án b: A → B → D → F → G
Có \(2.3.2.2 = 24\) cách đi;
Phương án c: A → C → D → E → G
Có \(3.4.2.5 = 120\) cách đi;
Phương án d: A → C → D → F → G
Có \(3.4.2.2 = 48\) cách đi.
Theo quy tắc cộng, ta có : \(60 + 24 + 120 + 48 = 252\) cách đi từ A đến G.
Câu 11 trang 63 SGK Đại số và Giải tích 11 Nâng cao thuộc chương trình học kỳ I, lớp 11. Bài toán này thường liên quan đến việc xét tính đơn điệu của hàm số, tìm cực trị, hoặc giải phương trình, bất phương trình chứa đạo hàm. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, các quy tắc tính đạo hàm, và các phương pháp xét tính đơn điệu của hàm số.
Trước khi bắt đầu giải, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Thông thường, đề bài sẽ yêu cầu chúng ta:
Để giải Câu 11 trang 63 SGK Đại số và Giải tích 11 Nâng cao, chúng ta có thể áp dụng các phương pháp sau:
Giả sử đề bài yêu cầu xét tính đơn điệu của hàm số f(x) = x3 - 3x2 + 2.
Bước 1: Tính đạo hàm
f'(x) = 3x2 - 6x
Bước 2: Xét dấu đạo hàm
f'(x) = 0 ⇔ 3x2 - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2
Xét các khoảng:
Bước 3: Kết luận
Hàm số f(x) đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2).
Khi giải các bài toán về đạo hàm, cần chú ý các điểm sau:
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự trong SGK và sách bài tập. Ngoài ra, bạn có thể tìm kiếm các bài tập trực tuyến trên các trang web học toán uy tín.
Câu 11 trang 63 SGK Đại số và Giải tích 11 Nâng cao là một bài toán quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc xét tính đơn điệu của hàm số. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày ở trên, bạn sẽ tự tin giải quyết bài toán này một cách hiệu quả.
| Khái niệm | Giải thích |
|---|---|
| Đạo hàm | Tốc độ thay đổi tức thời của hàm số. |
| Tính đơn điệu | Hàm số tăng hoặc giảm trên một khoảng. |
| Cực trị | Điểm mà hàm số đạt giá trị lớn nhất hoặc nhỏ nhất trong một khoảng. |