Bài tập này thường yêu cầu học sinh vận dụng kiến thức về vecto, các phép toán vecto và ứng dụng vào giải quyết các bài toán hình học không gian.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho đường tròn
Đề bài
Cho đường tròn (O; R) và điểm I cố định khác O. Một điểm M thay đổi trên đường tròn. Tia phân giác của góc MOI cắt IM tại N. Tìm quỹ tích điểm N
Lời giải chi tiết
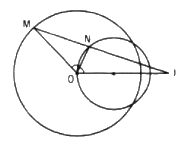
Đặt \(IO = d (d ≠ 0)\). Theo tính chất đường phân
giác của tam giác MOI, ta có:
\({{IN} \over {NM}} = {{IO} \over {OM}} = {d \over R}\)
Suy ra \({{IN} \over {IN + NM}} = {d \over {d + R}} \Leftrightarrow {{IN} \over {IM}} = {d \over {d + R}}\)
Vì hai vecto \(\overrightarrow {IN} \) và \(\overrightarrow {IM} \) cùng hướng nên đẳng
thức trên có nghĩa là:\(\overrightarrow {IN} = {d \over {d + R}}\overrightarrow {IM} \)
Nếu gọi V là phép vị tự tâm I tỉ số \(k = {d \over {d + R}}\) thì V biến điểm M thành điểm N
Khi M ở vị trí M0trên đường tròn (O ; R) sao cho \(\widehat {IO{M_0}} = {0^ \circ }\) thì tia phân giác của góc \(\widehat {IO{M_0}}\) không cắt IM. Điểm N không tồn tại.
Vậy khi M chạy trên (O ; R) (M khác hẳn M0) thì quỹ tích điểm N là ảnh của (O ; R) qua phép vị tự V bỏ đi ảnh của điểm M0
Câu 29 trang 29 SGK Hình học 11 Nâng cao thường liên quan đến việc xác định mối quan hệ giữa các vectơ trong không gian, hoặc chứng minh một đẳng thức vectơ nào đó. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Trước khi bắt tay vào giải bài toán, hãy đọc kỹ đề bài và xác định rõ yêu cầu. Phân tích các dữ kiện đã cho và tìm mối liên hệ giữa chúng. Vẽ hình minh họa (nếu cần thiết) để giúp bạn hình dung rõ hơn về bài toán.
(Giả sử đề bài Câu 29 trang 29 SGK Hình học 11 Nâng cao là: Cho hình hộp ABCD.A'B'C'D'. Gọi I là trung điểm của cạnh AB. Chứng minh rằng: vectơ AI = 1/2 vectơ AB + 1/2 vectơ AA'.)
Lời giải:
(Tiếp tục giải thích chi tiết các bước chứng minh, sử dụng các công thức và định lý liên quan đến vectơ. Ví dụ: Sử dụng quy tắc cộng vectơ, quy tắc trừ vectơ, và các tính chất của vectơ.)
Ngoài bài toán trên, còn rất nhiều dạng bài tập tương tự liên quan đến vectơ trong không gian. Một số dạng bài tập phổ biến bao gồm:
Để giải quyết các bài tập này, bạn cần nắm vững các kiến thức cơ bản về vectơ và luyện tập thường xuyên. Hãy bắt đầu với những bài tập đơn giản và dần dần nâng cao độ khó.
Câu 29 trang 29 SGK Hình học 11 Nâng cao là một bài tập quan trọng giúp bạn củng cố kiến thức về vectơ trong không gian. Bằng cách nắm vững các kiến thức cơ bản, phân tích bài toán một cách cẩn thận và luyện tập thường xuyên, bạn sẽ có thể giải quyết bài toán này một cách dễ dàng và hiệu quả. Chúc bạn học tốt!
| Khái niệm | Giải thích |
|---|---|
| Vectơ | Một đoạn thẳng có hướng, xác định bởi điểm gốc và điểm cuối. |
| Tích vô hướng | a.b = |a||b|cos(θ) |