Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, đặc biệt là các phép toán vectơ để giải quyết các vấn đề liên quan đến vị trí tương đối của các điểm và đường thẳng trong không gian.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho đường tròn (O ; R)
Đề bài
Cho đường tròn (O ; R) và điểm A cố định. Một dây cung BC thay đổi của (O ; R) có độ dài không đổi BC = m. Tìm quỹ tích các điểm G sao cho \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
Lời giải chi tiết
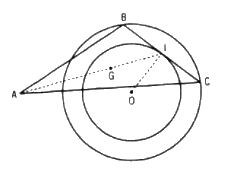
Gọi I là trung điểm của BC thì \(OI\bot BC\)
Ta có
\(\eqalign{& \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \cr & \Leftrightarrow \overrightarrow {GA} + 2\overrightarrow {GI} = \overrightarrow 0 \cr & \Leftrightarrow \overrightarrow {AG} = {2 \over 3}\overrightarrow {AI} \cr} \)
Tức là phép vị tự V tâm A tỉ số \({2 \over 3}\) biến điểm I thành điểm G
Trong tam giác vuông OIB ta có:
\(OI = \sqrt {O{B^2} - I{B^2}} \)\(= \sqrt {{R^2} - {{\left( {{m \over 2}} \right)}^2}} = R'\) (không đổi)
Nên quỹ tích I là đường tròn (O ; R’) hoặc là điểm O (nếu m = 2R)
Do đó quỹ tích G là ảnh của quỹ tích I qua phép vị tự V
Bài tập Câu 9 trang 35 SGK Hình học 11 Nâng cao thuộc chương trình học Hình học không gian, cụ thể là phần vectơ trong không gian. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Thông thường, bài tập này sẽ yêu cầu học sinh chứng minh một đẳng thức vectơ, xác định vị trí tương đối của các điểm hoặc đường thẳng, hoặc tính độ dài của một đoạn thẳng, góc giữa hai vectơ. Để giải quyết bài toán, học sinh cần:
Giả sử bài tập yêu cầu chứng minh rằng với ba điểm A, B, C bất kỳ, ta có: AB + BC = AC. Để chứng minh đẳng thức này, ta có thể sử dụng quy tắc cộng vectơ. Vectơ AB biểu diễn sự di chuyển từ A đến B, vectơ BC biểu diễn sự di chuyển từ B đến C. Do đó, vectơ AB + BC biểu diễn sự di chuyển từ A đến C, tức là vectơ AC. Vậy đẳng thức được chứng minh.
Để giải nhanh và hiệu quả các bài tập liên quan đến vectơ trong không gian, học sinh nên:
Ngoài SGK Hình học 11 Nâng cao, học sinh có thể tham khảo thêm các tài liệu sau:
Câu 9 trang 35 SGK Hình học 11 Nâng cao là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ trong không gian. Bằng cách nắm vững các kiến thức cơ bản, luyện tập thường xuyên và sử dụng các mẹo giải nhanh, học sinh có thể tự tin giải quyết bài tập này và các bài tập tương tự một cách hiệu quả.