Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, đồ thị hàm số và các phép biến đổi đồ thị để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin làm bài tập.
Xét hàm số y = f(x) = sinπx.
Chứng minh rằng với mỗi số nguyên chẵn \(m\) ta có \(f(x + m) = f(x)\) với mọi \(x\).
Lời giải chi tiết:
Đặt \(m = 2k, k \in\mathbb Z\). Ta có :
\(f(x + m) = \sinπ(x + m) \)
\(= \sin(πx + 2kπ) = \sinπx = f(x)\)
Lập bảng biến thiên của hàm số trên đoạn \([-1 ; 1]\).
Lời giải chi tiết:
Bảng biến thiên
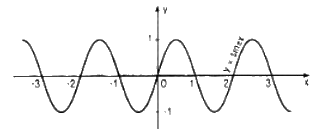
Vẽ đồ thị của hàm số đó.
Lời giải chi tiết:
Đồ thị

Câu 44 trang 47 SGK Đại số và Giải tích 11 Nâng cao thuộc chương trình học kỳ I, lớp 11. Bài toán này thường kiểm tra khả năng vận dụng các kiến thức về hàm số bậc hai, đặc biệt là việc xác định các yếu tố của parabol (đỉnh, trục đối xứng, điểm cắt trục hoành, điểm cắt trục tung) và sử dụng các tính chất của hàm số để giải quyết các bài toán thực tế.
Thông thường, câu 44 trang 47 sẽ yêu cầu học sinh thực hiện một trong các nhiệm vụ sau:
Để giải quyết hiệu quả câu 44 trang 47, học sinh cần nắm vững các kiến thức sau:
Bài toán: Xác định phương trình của parabol có đỉnh I(-1; 2) và đi qua điểm A(1; 0).
Lời giải:
Phương trình của parabol có dạng: y = a(x - xđỉnh)2 + yđỉnh.
Thay tọa độ đỉnh I(-1; 2) vào phương trình, ta được: y = a(x + 1)2 + 2.
Thay tọa độ điểm A(1; 0) vào phương trình, ta được: 0 = a(1 + 1)2 + 2 => 0 = 4a + 2 => a = -1/2.
Vậy phương trình của parabol là: y = -1/2(x + 1)2 + 2.
Khi giải các bài toán về hàm số bậc hai, học sinh cần chú ý:
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự trong SGK và sách bài tập Đại số và Giải tích 11 Nâng cao. Ngoài ra, bạn có thể tham khảo các bài giảng trực tuyến và các tài liệu học tập khác.
Câu 44 trang 47 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về hàm số bậc hai. Bằng cách nắm vững kiến thức và phương pháp giải, bạn có thể tự tin giải quyết các bài toán tương tự và đạt kết quả tốt trong học tập.