Giải Câu 35 Trang 68 SGK Hình Học 11 Nâng Cao

Câu 35 trang 68 SGK Hình học 11 Nâng cao

Câu 35 trang 68 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình Hình học 11 Nâng cao.

Bài toán này thường yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ, và ứng dụng vào hình học không gian.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và kỹ năng giải bài tập.

Cho hai điểm M, N lần lượt thay đổi trên hai mặt phẳng song song (P) và (Q). Tìm tập hợp các điểm I thuộc đoạn thẳng MN sao cho ({{IM} over {IN}} = k,k ne 0)cho trước

Đề bài

Cho hai điểm M, N lần lượt thay đổi trên hai mặt phẳng song song (P) và (Q). Tìm tập hợp các điểm I thuộc đoạn thẳng MN sao cho \({{IM} \over {IN}} = k,k \ne 0\)cho trước

Lời giải chi tiết

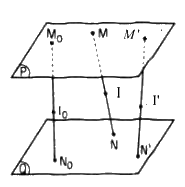
Câu 35 trang 68 SGK Hình học 11 Nâng cao 1

Thuận. Giả sử M \(\in\) (P), N \(\in\) (Q) và điểm I thuộc đoạn thẳng MN sao cho \({{IM} \over {IN}} = k.\)

Trên hai mặt phẳng (P) và (Q), ta lần lượt lấy hai điểm cố định M₀ và N₀ rồi lấy một điểm I₀ thuộc đoạn thẳng M₀N₀ sao cho \({{{M_0}{I_0}} \over {{N_0}{I_0}}} = k.\) Khi ấy điểm I₀ cố định.

Ta có: \({{IM} \over {IN}} = {{{I_0}{M_0}} \over {{I_0}{N_0}}}\left( { = k} \right)\)

\(\Rightarrow {{IM} \over {{I_0}{M_0}}} = {{IN} \over {{I_0}{N_0}}} = {{IM + IN} \over {{I_0}{M_0} + {I_0}{N_0}}} = {{MN} \over {{M_0}{N_0}}}\)

Áp dụng định lí Ta-lét đảo, ta suy ra đường thẳng I₀I thuộc một mặt phẳng (R) song song với (P) và (Q).

Mặt phẳng (R) cố định vì nó qua điểm cố định I₀ và song song với mặt phẳng cố định (P).

Vậy điểm I thuộc mặt phẳng (R) cố định.

Đảo. Ngược lại, lấy một điểm I’ bất kì trên mặt phẳng (R).

Qua I’ ta kẻ một đường thẳng cắt hai mặt phẳng (P) và (Q) lần lượt tại M’ và N’.

Xét hai cát tuyến M₀N₀ , M’N’ và ba mặt phẳng song song (P), (Q), (R).

Theo định lí Ta-lét ta có: \({{I'M'} \over {{I_0}{M_0}}} = {{I'N'} \over {{I_0}{N_0}}} = {{M'N'} \over {{M_0}{N_0}}}\)

Từ đó, ta suy ra I' thuộc đoạn thẳng M’N’ và \({{I'M'} \over {I'N'}} = {{{I_0}{M_0}} \over {{I_0}{N_0}}} = k\)

Kết luận: Tập hợp điểm I thuộc đoạn thẳng MN sao cho \({{IM} \over {IN}} = k\) là mặt phẳng (R) nói trên.

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Câu 35 trang 68 SGK Hình học 11 Nâng cao – hành trang không thể thiếu trong chuyên mục Bài tập Toán lớp 11 trên nền tảng soạn toán. Bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải chi tiết Câu 35 trang 68 SGK Hình học 11 Nâng cao

Câu 35 trang 68 SGK Hình học 11 Nâng cao thuộc chương trình học Hình học 11, tập trung vào việc vận dụng kiến thức về vectơ trong không gian để giải quyết các bài toán liên quan đến quan hệ song song, vuông góc giữa đường thẳng và mặt phẳng. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về vectơ, tích vô hướng, tích có hướng, và các định lý liên quan.

Phân tích đề bài và xác định yêu cầu

Trước khi bắt đầu giải bài toán, điều quan trọng là phải đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Thông thường, đề bài sẽ cung cấp thông tin về các điểm, đường thẳng, mặt phẳng trong không gian, và yêu cầu chứng minh một mối quan hệ nào đó giữa chúng. Việc phân tích đề bài chính xác sẽ giúp học sinh lựa chọn phương pháp giải phù hợp và tránh sai sót.

Áp dụng kiến thức về vectơ

Vectơ là công cụ quan trọng để giải quyết các bài toán hình học không gian. Để giải Câu 35 trang 68, học sinh cần sử dụng các kiến thức sau:

Khái niệm vectơ: Vectơ là một đoạn thẳng có hướng, được xác định bởi điểm gốc và điểm cuối.
Các phép toán vectơ: Cộng, trừ, nhân với một số thực.
Tích vô hướng:a.b = |a||b|cos(θ), dùng để tính góc giữa hai vectơ và kiểm tra tính vuông góc.
Tích có hướng:a x b, dùng để tìm vectơ pháp tuyến của mặt phẳng và kiểm tra tính song song.

Phương pháp giải bài toán

Có nhiều phương pháp để giải Câu 35 trang 68, tùy thuộc vào yêu cầu cụ thể của bài toán. Một số phương pháp thường được sử dụng bao gồm:

Phương pháp tọa độ: Chọn hệ tọa độ thích hợp và biểu diễn các điểm, vectơ bằng tọa độ. Sau đó, sử dụng các công thức tính tích vô hướng, tích có hướng để giải quyết bài toán.
Phương pháp hình học: Sử dụng các định lý, tính chất hình học để chứng minh các mối quan hệ giữa các yếu tố đã cho.
Phương pháp vectơ: Sử dụng các phép toán vectơ để chứng minh các mối quan hệ song song, vuông góc.

Ví dụ minh họa (giả định một dạng bài tập cụ thể)

Giả sử đề bài yêu cầu chứng minh rằng hai đường thẳng song song với nhau. Ta có thể sử dụng phương pháp vectơ như sau:

Cho hai đường thẳng d1 và d2, vectơ chỉ phương của d1 là u1, vectơ chỉ phương của d2 là u2. Để chứng minh d1 song song với d2, ta cần chứng minh rằng u1 = k.u2 với k là một số thực khác 0.

Lưu ý khi giải bài tập

Khi giải Câu 35 trang 68 và các bài tập tương tự, học sinh cần lưu ý những điều sau:

Đọc kỹ đề bài và xác định rõ yêu cầu.
Nắm vững các khái niệm, định lý liên quan.
Lựa chọn phương pháp giải phù hợp.
Kiểm tra lại kết quả sau khi giải xong.

Ứng dụng của bài toán

Kiến thức về vectơ và các phép toán vectơ có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, như vật lý, kỹ thuật, đồ họa máy tính. Việc nắm vững kiến thức này sẽ giúp học sinh có nền tảng vững chắc để học tập và làm việc trong tương lai.

Bài tập tương tự

Để củng cố kiến thức, học sinh có thể làm thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập.

Kết luận

Câu 35 trang 68 SGK Hình học 11 Nâng cao là một bài toán quan trọng, giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về vectơ vào giải quyết các bài toán hình học không gian. Hy vọng với lời giải chi tiết và các lưu ý trên, học sinh có thể tự tin giải quyết bài toán này và các bài tập tương tự.