Chào mừng bạn đến với bài giải chi tiết Câu 6 trang 34 SGK Hình học 11 Nâng cao trên giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải chính xác, dễ hiểu cùng với phương pháp giải bài tập để giúp bạn nắm vững kiến thức và tự tin giải các bài toán tương tự.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất cho học sinh, sinh viên và những người yêu thích môn Toán.
Gọi F là phép biến hình có tính chất sau đây
Đề bài
Gọi F là phép biến hình có tính chất sau đây: Với mọi cặp điểm M, N và ảnh M’, N’ của chúng, ta luôn có \(\overrightarrow {M'N'} = k\overrightarrow {MN} \) , trong đó k là một số không đổi khác 0. Hãy chứng minh rằng F là phép tịnh tiến hoặc phép vị tự
Lời giải chi tiết
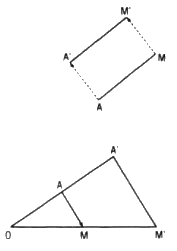
Ta lấy một điểm A cố định và đặt A’ = F(A)
Theo giả thiết, với điểm M bất kì và ảnh M’ =F(M) của nó, ta có \(\overrightarrow {A'M'} = k\overrightarrow {AM} \)
Nếu k = 1, thì \(\overrightarrow {A'M'} = \overrightarrow {AM} \), do đó \(\overrightarrow {MM'} =\overrightarrow {AA'} \) ,và F là phép tịnh tiến theo vecto \(\overrightarrow {AA'} \)
Nếu k ≠ 1 thì có điểm O sao cho:
\(\overrightarrow {OA'} = k\overrightarrow {OA} \) (với O thỏa \(\overrightarrow {OA} = {1 \over {1 - k}}\overrightarrow {AA'} \) )
Khi đó ta có:
\(\overrightarrow {OM'} = \overrightarrow {OA'} + \overrightarrow {A'M'} = k\overrightarrow {OA} + k\overrightarrow {AM} = k\overrightarrow {OM} \)
Vậy F là phép vị tự tâm O, tỉ số k
Câu 6 trang 34 SGK Hình học 11 Nâng cao thường xoay quanh các kiến thức về vectơ trong không gian, đặc biệt là các phép toán vectơ, tính chất của vectơ, và ứng dụng của vectơ trong việc chứng minh các đẳng thức hình học.
(Nội dung đề bài cụ thể sẽ được chèn vào đây. Ví dụ: Cho hình hộp ABCD.A'B'C'D'. Gọi M là trung điểm của cạnh AB. Chứng minh rằng vectơ AM = 1/2 vectơ AB.)
Để giải quyết bài toán này, chúng ta cần nắm vững các kiến thức sau:
Phương pháp giải thường được sử dụng là:
(Lời giải chi tiết, từng bước, có giải thích rõ ràng sẽ được trình bày ở đây. Ví dụ:)
Gọi A là gốc tọa độ, AB là trục x, AD là trục y, và AA' là trục z. Khi đó, ta có:
Suy ra, vectơ AM = (a/2, 0, 0) và vectơ AB = (a, 0, 0). Do đó, vectơ AM = 1/2 vectơ AB (đpcm).
Để hiểu rõ hơn về cách giải các bài toán liên quan đến vectơ trong không gian, chúng ta hãy xem xét một số ví dụ minh họa sau:
(Các ví dụ minh họa và bài tập tương tự sẽ được trình bày ở đây, kèm theo lời giải chi tiết.)
Ngoài các kiến thức đã trình bày ở trên, bạn có thể tìm hiểu thêm về:
Hy vọng rằng bài giải chi tiết Câu 6 trang 34 SGK Hình học 11 Nâng cao trên giaitoan.edu.vn đã giúp bạn hiểu rõ hơn về cách giải các bài toán liên quan đến vectơ trong không gian. Chúc bạn học tập tốt!
| Khái niệm | Giải thích |
|---|---|
| Vectơ | Một đoạn thẳng có hướng. |
| Tích vô hướng | Một phép toán giữa hai vectơ cho ra một số thực. |
| Tích có hướng | Một phép toán giữa hai vectơ cho ra một vectơ vuông góc với cả hai vectơ ban đầu. |