Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác các bài tập trong sách giáo khoa Hình học 11 Nâng cao.
Trong bài viết này, chúng ta sẽ cùng nhau giải quyết Câu 38 trang 68 SGK Hình học 11 Nâng cao, một bài tập quan trọng giúp bạn hiểu sâu hơn về kiến thức đã học.
Hãy cùng bắt đầu với việc phân tích đề bài và tìm ra phương pháp giải phù hợp nhất nhé!
Chứng minh rẳng tổng bình phương tất cả các đường chéo của một hình hộp bằng tổng bình phương tất cả các cạnh của hình hộp đó
Đề bài
Chứng minh rẳng tổng bình phương tất cả các đường chéo của một hình hộp bằng tổng bình phương tất cả các cạnh của hình hộp đó
Phương pháp giải - Xem chi tiết
Áp dụng tính chất: “ Trong một hình bình hành, tổng bình phương hai đường chéo bằng tổng bình phương bốn cạnh.”
Chứng minh:
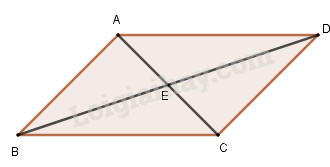
Ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2AB.BC\cos B\\B{D^2} = A{B^2} + A{D^2} - 2AB.AD\cos A\\\,\,\,\,\,\,\,\,\,\,\, = A{B^2} + B{C^2} + 2AB.BC\cos B\end{array}\)
Vì \(AD = BC\) và \(\cos A = - \cos B\) (hai góc bù nhau thì cos đối nhau)
\( \Rightarrow A{C^2} + B{D^2} = 2A{B^2} + 2B{C^2}\) \( = 2\left( {A{B^2} + B{C^2}} \right)\).
Lời giải chi tiết
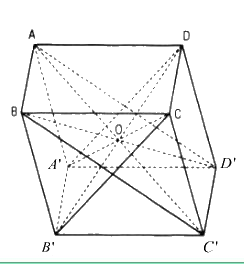
Đặt AB = a, BC = b, AA’ = c ( đó là 3 kích thước của hình hộp).
Trong hình bình hành ABC’D’ ta có:
\(AC'{^2} + BD{'^2} = 2\left( {{a^2} + BC'{^2}} \right)\) (1)
Trong hình bình hành A’B’CD ta có:
\(A'{C^2} + B'{D^2} = 2\left( {{a^2} + B'{C^2}} \right)\) (2)
Cộng (1) và (2) ta được :
\(AC'{^2} + BD'{^2}+A'{C^2} + B'{D^2} \)\(= 2\left( {2{a^2} + BC{'^2} + B'{C^2}} \right)\) (3)
Mặt khác trong hình bình hành BB’C’C ta có:
\(BC{'^2} + B'{C^2} = 2\left( {{b^2} + {c^2}} \right)\) (4)
Thay (4) vào (3) ta được :
\(AC'{^2} + BD'{^2} + A'{C^2} + B\,'{D^2}\)\( = 4\left( {{a^2} + {b^2} + {c^2}} \right)\) (đpcm).
Câu 38 trang 68 SGK Hình học 11 Nâng cao thường liên quan đến các kiến thức về vectơ, đặc biệt là các phép toán vectơ trong không gian. Để giải quyết bài toán này, học sinh cần nắm vững các khái niệm cơ bản như:
Dưới đây là một ví dụ về dạng bài tập thường gặp và cách giải chi tiết:
Đề bài: Cho hai điểm A(1; 2; 3) và B(3; 4; 5). Tính độ dài đoạn thẳng AB và tìm tọa độ trung điểm I của đoạn thẳng AB.
Giải:
Kết luận: Độ dài đoạn thẳng AB là 2√3 và tọa độ trung điểm I của đoạn thẳng AB là (2; 3; 4).
Ngoài dạng bài tập tính độ dài và tìm trung điểm, Câu 38 trang 68 SGK Hình học 11 Nâng cao còn có thể xuất hiện các dạng bài tập sau:
Để giải tốt các bài tập về vectơ trong không gian, bạn nên:
Để củng cố kiến thức và kỹ năng giải bài tập, bạn có thể tham khảo thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Ngoài ra, bạn cũng có thể tìm kiếm các bài giải trực tuyến trên giaitoan.edu.vn để học hỏi kinh nghiệm và phương pháp giải của những người khác.
| Công Thức | Mô Tả |
|---|---|
| |AB| = √((xB - xA)² + (yB - yA)² + (zB - zA)²) | Độ dài đoạn thẳng AB |
| I = ((xA + xB)/2; (yA + yB)/2; (zA + zB)/2) | Tọa độ trung điểm I của đoạn thẳng AB |
| a.b = |a||b|cos(θ) | Tích vô hướng của hai vectơ a và b |
Hy vọng với những giải thích chi tiết và ví dụ minh họa trên, bạn đã hiểu rõ hơn về cách giải Câu 38 trang 68 SGK Hình học 11 Nâng cao. Chúc bạn học tập tốt và đạt kết quả cao trong môn Hình học!