Bài toán này thường yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ, và ứng dụng vào hình học không gian.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. a. Chứng minh rằng AC’ vuông góc với hai mặt phẳng (A’BD) và (B’CD’). b. Cắt hình lập phương bởi mặt phẳng trung trực của AC’. Chứng minh thiết diện tạo thành là một lục giác đều. Tính diện tích thiết diện đó.
Đề bài
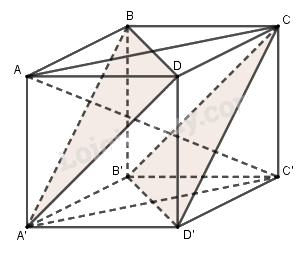
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a.
a. Chứng minh rằng AC’ vuông góc với hai mặt phẳng (A’BD) và (B’CD’).
b. Cắt hình lập phương bởi mặt phẳng trung trực của AC’. Chứng minh thiết diện tạo thành là một lục giác đều. Tính diện tích thiết diện đó.
Lời giải chi tiết
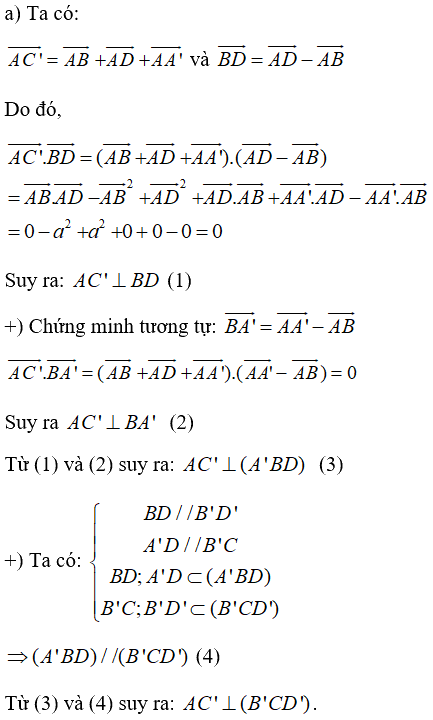
Cách khác:
Ta có: \(BD \bot AC\) (do \(ABCD\) là hình vuông)
\(BD \bot AA'\) (do \(AA' \bot \left( {ABCD} \right)\))
\( \Rightarrow BD \bot \left( {ACC'A'} \right)\) \( \Rightarrow BD \bot AC'\)
\(\left\{ \begin{array}{l}A'D \bot AD'\\A'D \bot AB\end{array} \right. \Rightarrow A'D \bot \left( {ABC'D'} \right)\)
\( \Rightarrow A'D \bot AC'\)
Ta có: \(\left\{ \begin{array}{l}BD \bot AC'\\A'D \bot AC'\end{array} \right.\) \( \Rightarrow AC' \bot \left( {A'BD} \right)\)
Lại có, \(\left\{ \begin{array}{l}BD//B'D'\\A'B//CD'\\BD,A'B \subset \left( {A'BD} \right)\\B'D',CD' \subset \left( {CB'D'} \right)\end{array} \right.\) \( \Rightarrow \left( {A'BD} \right)//\left( {CB'D'} \right)\)
\( \Rightarrow AC' \bot \left( {CB'D'} \right)\)
Vậy \(AC'\) vuông góc với các mặt phẳng \(\left( {A'BD} \right)\) và \(\left( {CB'D'} \right)\).
b)
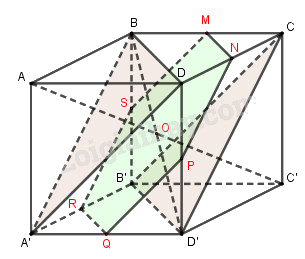
Gọi \(O\) là trung điểm của \(AC'\).
\(\left( P \right)\) là mặt phẳng trung trực của \(AC'\) thì \(\left( P \right)\) đi qua \(O\) và vuông góc với \(AC'\).
Mà \(AC'//\left( {A'BD} \right)\) và \(AC' \bot \left( {CB'D'} \right)\) nên \(\left( P \right)//\left( {A'BD} \right)//\left( {CB'D'} \right)\).
Ta có: \(\left\{ \begin{array}{l}BD \subset \left( {BDD'B'} \right)\\BD//\left( P \right)\\O \in \left( P \right) \cap \left( {BDD'B'} \right)\end{array} \right.\) \( \Rightarrow \left( P \right) \cap \left( {BDD'B'} \right) = Ot//BD\)
Trong \(\left( {BDD'B'} \right)\), qua \(O\) kẻ đường thẳng \(Ot//BD\) và cắt \(BB',DD'\) lần lượt tại các điểm \(S,P\).
Tương tự,
\(\left\{ \begin{array}{l}A'D \subset \left( {ADD'A'} \right)\\A'D//\left( P \right)\\P \in \left( P \right) \cap \left( {ADD'A'} \right)\end{array} \right.\) \( \Rightarrow \left( P \right) \cap \left( {ADD'A'} \right) = PQ//A'D\) với \(Q \in A'D\).
\(\left\{ \begin{array}{l}B'D \subset \left( {A'B'C'D'} \right)\\B'D//\left( P \right)\\Q \in \left( P \right) \cap \left( {A'B'C'D'} \right)\end{array} \right.\) \( \Rightarrow \left( P \right) \cap \left( {A'B'C'D'} \right) = QR//B'D'\) với \(R \in A'B'\).
\(\left\{ \begin{array}{l}CD' \subset \left( {CDD'C'} \right)\\CD'//\left( P \right)\\P \in \left( P \right) \cap \left( {CDD'C'} \right)\end{array} \right.\) \( \Rightarrow \left( P \right) \cap \left( {CDD'C'} \right) = PN//CD'\) với \(N \in CD\).
\(\left\{ \begin{array}{l}BD \subset \left( {ABCD} \right)\\BD//\left( P \right)\\N \in \left( P \right) \cap \left( {ABCD} \right)\end{array} \right.\) \( \Rightarrow \left( P \right) \cap \left( {ABCD} \right) = NM//BD\) với \(M \in BC\).
Vậy thiết diện là lục giác \(MNPQRS\).
Dễ thấy, \(O\) là trung điểm của \(AC'\) nên cũng là trung điểm của \(BD'\).
\( \Rightarrow PS//BD\) thì \(P,S\) lần lượt là trung điểm của \(DD',BB'\).
Từ đó các điểm \(M,N,Q,R\) lần lượt là trung điểm của \(BC,CD,D'A',A'B'\).
\(ABCD\) là hình vuông cạnh \(a\) nên \(BD = \sqrt {A{B^2} + A{D^2}} \) \( = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\( \Rightarrow MN = \frac{1}{2}BD = \frac{{a\sqrt 2 }}{2}\)
Tương tự \(MN = NP = PQ\) \( = QR = RS = SM = \frac{{a\sqrt 2 }}{2}\).
Do đó, lục giác \(MNPQRS\) là lục giác đều.
Xét \(\Delta MON\) đều cạnh \(OM = ON = MN = \frac{{a\sqrt 2 }}{2}\) nên có diện tích:
\({S_{MON}} = \frac{1}{2}OM.ON.\sin \widehat {MON}\) \( = \frac{1}{2}.\frac{{a\sqrt 2 }}{2}.\frac{{a\sqrt 2 }}{2}.\sin {60^0} = \frac{{{a^2}\sqrt 3 }}{8}\)
Vậy \({S_{MNPQRS}} = 6{S_{MON}}\) \( = 6.\frac{{{a^2}\sqrt 3 }}{8} = \frac{{3{a^2}\sqrt 3 }}{4}\).
Câu 23 trang 111 SGK Hình học 11 Nâng cao thường liên quan đến việc xác định mối quan hệ giữa các vectơ trong không gian, tính toán độ dài vectơ, tích vô hướng, và ứng dụng vào việc chứng minh các tính chất hình học.
Trước khi bắt đầu giải, cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Vẽ hình minh họa (nếu cần thiết) để hình dung rõ hơn về bài toán.
Để giải quyết bài toán này, bạn cần nắm vững các kiến thức sau:
(Phần này sẽ chứa lời giải chi tiết của bài toán, bao gồm các bước giải, giải thích rõ ràng, và kết luận.)
Ví dụ, giả sử đề bài yêu cầu chứng minh một tứ giác là hình bình hành. Bạn có thể sử dụng tính chất của vectơ để chứng minh rằng hai cặp cạnh đối song song hoặc hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Ví dụ 1: Cho hình hộp ABCD.A'B'C'D'. Gọi M là trung điểm của cạnh AB. Chứng minh rằng vectơ MM' vuông góc với mặt phẳng (ABCD).
Lời giải:
Để củng cố kiến thức, bạn có thể giải các bài tập tương tự sau:
Câu 23 trang 111 SGK Hình học 11 Nâng cao là một bài toán quan trọng, giúp bạn rèn luyện kỹ năng giải toán vectơ và ứng dụng vào hình học không gian. Hy vọng với lời giải chi tiết và các kiến thức liên quan được cung cấp, bạn sẽ tự tin giải quyết bài toán này và các bài toán tương tự.
| Công Thức | Mô Tả |
|---|---|
| a.b = |a||b|cos(θ) | Tích vô hướng của hai vectơ a và b |
| |a| = √(x2 + y2 + z2) | Độ dài của vectơ a |