Bài toán này thường yêu cầu học sinh vận dụng kiến thức về hàm số, đạo hàm, hoặc các khái niệm khác đã học để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Tính các giới hạn sau :
\(\lim \sqrt {3{n^4} - 10n + 12} \)
Lời giải chi tiết:
\(\lim \sqrt {3{n^4} - 10n + 12} \) \(= \lim {n^2}.\sqrt {3 - {{10} \over {{n^3}}} + {{12} \over {{n^4}}}} \) \(= + \infty \)
Vì
\(\left\{ \begin{array}{l}\lim {n^2} = + \infty \\\lim \sqrt {3 - \frac{{10}}{{{n^3}}} + \frac{{12}}{{{n^4}}}} = \sqrt 3 > 0\end{array} \right.\)
\(\lim \left( {{{2.3}^n} - {{5.4}^n}} \right)\)
Lời giải chi tiết:
\(\lim \left( {{{2.3}^n} - {{5.4}^n}} \right) \) \(= \lim {4^n}\left[ {2{{\left( {{3 \over 4}} \right)}^n} - 5} \right] = - \infty \)
Vì
\(\left\{ \begin{array}{l}\lim {4^n} = + \infty \\\lim \left( {2.{{\left( {\frac{3}{4}} \right)}^n} - 5} \right) = - 5 < 0\end{array} \right.\)
\(\lim \left( {\sqrt {{n^4} + {n^2} + 1} - {n^2}} \right)\)
Lời giải chi tiết:
\(\eqalign{ & \lim \left( {\sqrt {{n^4} + {n^2} + 1} - {n^2}} \right) \cr& = \lim \frac{{\left( {\sqrt {{n^4} + {n^2} + 1} - {n^2}} \right)\left( {\sqrt {{n^4} + {n^2} + 1} + {n^2}} \right)}}{{\sqrt {{n^4} + {n^2} + 1} + {n^2}}} \cr &= \lim \frac{{{n^4} + {n^2} + 1 - {n^4}}}{{\sqrt {{n^4} + {n^2} + 1} + {n^2}}}\cr &= \lim {{{n^2} + 1} \over {\sqrt {{n^4} + {n^2} + 1} + {n^2}}} \cr & = \lim \frac{{{n^2} + 1}}{{\sqrt {{n^4}\left( {1 + \frac{1}{{{n^2}}} + \frac{1}{{{n^4}}}} \right)} + {n^2}}} \cr & = \lim \frac{{{n^2}\left( {1 + \frac{1}{{{n^2}}}} \right)}}{{{n^2}\sqrt {1 + \frac{1}{{{n^2}}} + \frac{1}{{{n^4}}}} + {n^2}}} \cr & = \lim \frac{{{n^2}\left( {1 + \frac{1}{{{n^2}}}} \right)}}{{{n^2}\left( {\sqrt {1 + \frac{1}{{{n^2}}} + \frac{1}{{{n^4}}}} + 1} \right)}}\cr & = \lim {{1 + {1 \over {{n^2}}}} \over {\sqrt {1 + {1 \over {{n^2}}} + {1 \over {{n^4}}}} + 1}} \cr & = \frac{{1 + 0}}{{\sqrt {1 + 0 + 0} + 1}}= {1 \over 2} \cr} \)
\(\lim {1 \over {\sqrt {{n^2} + 2n} - n}}\)
Lời giải chi tiết:
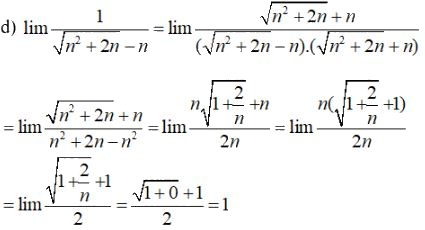
Câu 17 trang 226 SGK Đại số và Giải tích 11 Nâng cao thường thuộc vào các chủ đề về đạo hàm, ứng dụng đạo hàm để khảo sát hàm số, hoặc các bài toán liên quan đến bất đẳng thức. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản và kỹ năng giải toán liên quan.
Trước khi bắt đầu giải, hãy đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Xác định các thông tin đã cho, các điều kiện ràng buộc và mục tiêu cần đạt được. Việc phân tích đề bài chính xác sẽ giúp bạn lựa chọn phương pháp giải phù hợp.
Tùy thuộc vào nội dung cụ thể của câu 17, phương pháp giải có thể khác nhau. Dưới đây là một số phương pháp thường được sử dụng:
(Ở đây sẽ là lời giải chi tiết của câu 17 trang 226, bao gồm các bước giải, giải thích rõ ràng và kết luận. Ví dụ, nếu bài toán yêu cầu tìm đạo hàm của hàm số f(x) = x^2 + 2x + 1, lời giải sẽ như sau:)
f'(x) = lim (h->0) [f(x+h) - f(x)] / h
f'(x) = lim (h->0) [(x+h)^2 + 2(x+h) + 1 - (x^2 + 2x + 1)] / h
f'(x) = lim (h->0) [x^2 + 2xh + h^2 + 2x + 2h + 1 - x^2 - 2x - 1] / h
f'(x) = lim (h->0) [2xh + h^2 + 2h] / h
f'(x) = lim (h->0) [2x + h + 2]
f'(x) = 2x + 2
Để hiểu rõ hơn về cách giải, chúng ta hãy xem xét một ví dụ minh họa. (Ví dụ sẽ tương tự như câu 17, nhưng có thể đơn giản hơn để dễ hiểu)
Khi giải các bài toán về đạo hàm, cần chú ý đến các điểm sau:
Để củng cố kiến thức, bạn có thể thử giải các bài tập tương tự sau:
Câu 17 trang 226 SGK Đại số và Giải tích 11 Nâng cao là một bài toán quan trọng giúp học sinh rèn luyện kỹ năng giải toán về đạo hàm và ứng dụng đạo hàm. Bằng cách nắm vững kiến thức cơ bản, áp dụng phương pháp giải phù hợp và luyện tập thường xuyên, bạn có thể tự tin giải quyết bài toán này và các bài toán tương tự.