Chào mừng bạn đến với bài giải chi tiết Câu 5 trang 120 SGK Hình học 11 Nâng cao trên giaitoan.edu.vn. Bài tập này thuộc chương trình Hình học không gian, tập trung vào việc vận dụng kiến thức về vectơ, đường thẳng và mặt phẳng trong không gian.
Chúng tôi cung cấp lời giải dễ hiểu, phương pháp giải rõ ràng, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = a, OB = b, OC = c. Gọi H là hình chiếu của O trên mặt phẳng (ABC). Tính diện tích các tam giác HAB, HBC và HCA.
Đề bài
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = a, OB = b, OC = c. Gọi H là hình chiếu của O trên mặt phẳng (ABC). Tính diện tích các tam giác HAB, HBC và HCA.
Lời giải chi tiết
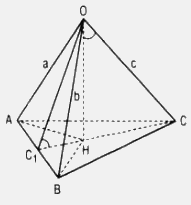
Vì OA, OB, OC đôi một vuông góc và H là hình chiếu của O trên mp(ABC) nên H là trực tâm tam giác ABC. Từ đó HC1 ⊥ AB (C1 là giao điểm của CH và AB), suy ra OC1 ⊥ AB. Như vậy \(\widehat {O{C_1}H}\) là góc giữa mp(OAB) và mp(ABC).
Ta có: \({S_{HAB}} = {S_{OAB}}\cos \widehat {O{C_1}H}\)
Mà \(\widehat {O{C_1}H} = \widehat {HOC}\) nên \({S_{HAB}} = {S_{OAB}}\cos \widehat {HOC}.\)
Ta lại có : \(\cos \widehat {HOC} = {{OH} \over {OC}},{1 \over {O{H^2}}} = {1 \over {O{A^2}}} + {1 \over {O{B^2}}} + {1 \over {O{C^2}}}\)
Từ đó : \(\cos \widehat {HOC} = {{ab} \over {\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}\)
Mặt khác \({S_{OAB}} = {1 \over 2}ab\)
Vậy \({S_{HAB}} = {{{a^2}{b^2}} \over {2\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}\)
Tương tự như trên, ta có :
\(\eqalign{ & {S_{HBC}} = {{{b^2}{c^2}} \over {2\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }} \cr & {S_{HAC}} = {{{c^2}{a^2}} \over {2\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }} \cr} \)
Câu 5 trang 120 SGK Hình học 11 Nâng cao yêu cầu học sinh vận dụng kiến thức về vectơ để chứng minh một đẳng thức vectơ liên quan đến các điểm và vectơ trong không gian. Để giải bài tập này, chúng ta cần nắm vững các quy tắc cộng, trừ vectơ, quy tắc nhân vectơ với một số thực, và các tính chất của vectơ.
Đề bài thường cho một hình không gian với các điểm A, B, C, D,... và các vectơ liên quan. Yêu cầu là chứng minh một đẳng thức vectơ, ví dụ như AB + CD = AD. Việc phân tích đề bài giúp xác định rõ các vectơ cần sử dụng và mối quan hệ giữa chúng.
Giả sử đề bài: Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng AB + AD + AA' = AC'.
Lời giải:
Khi giải các bài tập về vectơ trong không gian, cần chú ý:
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự trong SGK và sách bài tập Hình học 11 Nâng cao. Ngoài ra, bạn có thể tìm kiếm thêm các bài tập trực tuyến trên giaitoan.edu.vn.
Câu 5 trang 120 SGK Hình học 11 Nâng cao là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về vectơ trong không gian. Hy vọng với lời giải chi tiết và phương pháp giải rõ ràng trên đây, bạn đã nắm vững kiến thức và tự tin giải các bài tập tương tự.
| Khái niệm | Giải thích |
|---|---|
| Vectơ | Một đoạn thẳng có hướng. |
| Cộng vectơ | Quy tắc hình bình hành hoặc quy tắc tam giác. |
| Tích của một số thực với một vectơ | Làm thay đổi độ dài của vectơ. |